The area of the triangle formed by the intersection of a line parallel to x-axis and passing through P (h, k) with the lines y = x and x + y = 2 is $4 h^{2}$ . Find the locus of the point P.

Video Solution

Text Solution

Verified by Experts

Here, the triangle formed by a line parallel to $X$ -axis passing through $P (h, k)$ and the straight line $y = x$ and $y = 2 - x$ could be as shown below :

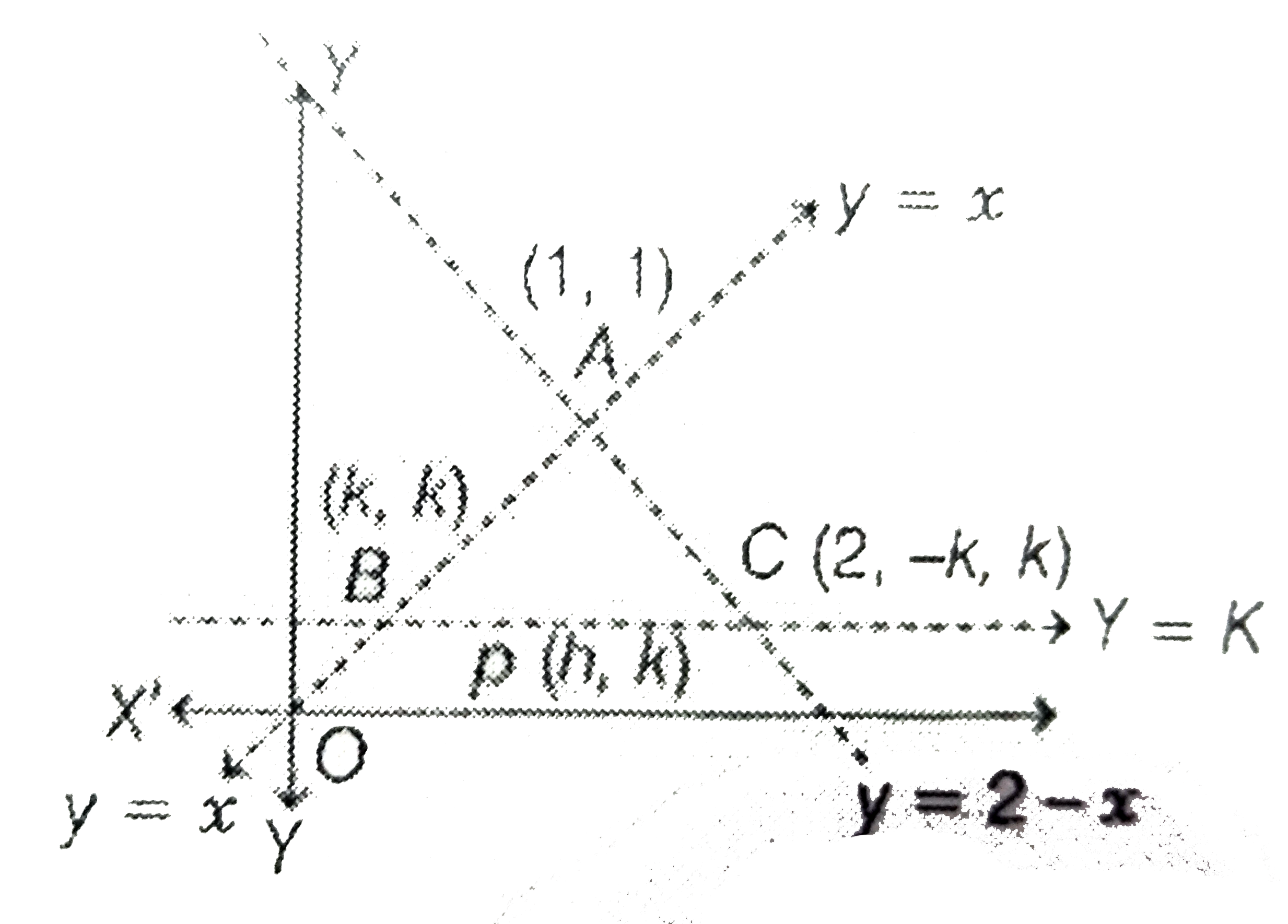
Since, area of $Δ A B C = 4 h^{2}$
$∴ \frac{1}{2} A B \cdot A C = 4 h^{2}$
where, $A B = \sqrt{2} | k - 1 |$ and $A C = \sqrt{2} (| k - 1 |)$
$\Rightarrow \frac{1}{2} \cdot 2 {(k - 1)}^{2} = 4 h^{2}$
$\Rightarrow 4 h^{2} = {(k - 1)}^{2}$
$\Rightarrow 2 h = \pm (k - 1)$
The locus of a point is $2 x = \pm (y - 1)$ .

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE AND PAIR OF STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The area of the triangle formed by the intersection of a line parallel to x-axis and passing through P(h,k), with the lines y=x and $x + y = 2$ is $h^{2}$ . The locus of the point P is
A $x = y - 1$
B $x = - (y - 1)$
C $x = 1 + y$
D $x = - (1 + y)$

IIT JEE PREVIOUS YEAR-STRAIGHT LINE AND PAIR OF STRAIGHT LINES-ANGLE BETWEEN STRAIGHT LINE AND EQUATION OF ANGLE BISECTOR (Analytical & Desriptive Questions)

Home
Ask Doubt
Profile