The equilibtium for the dissociation of XY2 is given as,
2XY2(g)⇔2XY(g)+Y2(g)
if the degree of dissociation x is so small compared to one. Show that 2KP=Px3 where P is the total pressure and KP is the dissociation equilibrium constant of XY2.
2XY2(g)⇔2XY(g)+Y2(g)
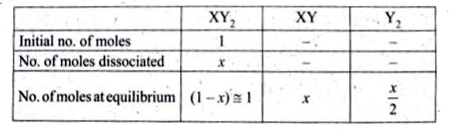
Total No. moles =1−x+x+x2=1+x2≅1
[∴ Given that x<<1,1−x≅1and1+x2≅1]
KP=(PXY)2(PY2)(PXY2)2=(x1×P)2(x21×P)(11×P)2
KP=x3P2⇒2KP=x3P
Topper's Solved these Questions
- PHYSICAL AND CHEMICAL EQUILIBRIUMBOOK - FULL MARKSCHAPTER - PHYSICAL AND CHEMICAL EQUILIBRIUMEXERCISE - ADDITIONAL QUESTIONS SOLVED (CHOOSE THE CORRECT ANSWER)
40 Videos
- PHYSICAL AND CHEMICAL EQUILIBRIUMBOOK - FULL MARKSCHAPTER - PHYSICAL AND CHEMICAL EQUILIBRIUMEXERCISE - ADDITIONAL QUESTIONS SOLVED (MATCH THE FOLLOWING)
5 Videos
- PHYSICAL AND CHEMICAL EQUILIBRIUMBOOK - FULL MARKSCHAPTER - PHYSICAL AND CHEMICAL EQUILIBRIUMEXERCISE - TEXTUAL EVALUATION SOLVED (SHORT ANSWER QUESTIONS)
10 Videos
- PERIODIC CLASSIFICATION OF ELEMENTS BOOK - FULL MARKSCHAPTER - PERIODIC CLASSIFICATION OF ELEMENTS EXERCISE - Activity 3.2
1 Videos
- QUANTUM MECHANICAL MODEL OF ATOMBOOK - FULL MARKSCHAPTER - QUANTUM MECHANICAL MODEL OF ATOMEXERCISE - Additional Questions Solved (5-Mark Questions)
6 Videos
Similar Questions
The dissociation equilibrium of a gas AB2 can be represented as, 2AB2(g)⇔2AB(g)+B2(g). The degree of disssociation is 'x' and is small compared to 1. The expression relating the degree of dissociation (x) with equilibrium constant kp and total pressure P is
View SolutionAt temperature T, a compound AB2(g) dissociation according to the reaction, 2AB2(g)⇔2AB(g)+B2(g) with degree of dissociation, α, which is small compared to unity . Deduce the expression for α in terms of the equilibrium constant Kp and the total pressure P.
View Solution
Knowledge Check
The dissociation equilibrium of a gas AB2 can be represented as, 2AB2(g)⇔2AB(g)+B2(g). The degree of disssociation is 'x' and is small compared to 1. The expression relating the degree of dissociation (x) with equilibrium constant kp and total pressure P is
A(KpP)B(2kpP)C(2KpP)1/3D(2KpP)1/2At a certain temperature T, a compound AB4(g) dissociates as 2AB4(g)⇔A2(g)+4B2(g) with a degree of dissociation x, which is very small as compared to unity. The expression of Kp interms of x and total equilibrium pressure p is-
A8P3x5B256P3x5C4Px2DNone of theseThe dissociation equilibrium of a gas AB2 can be represented as, 2AB2(g)⇔2AB(g)+B2(g). The degree of disssociation is 'x' and is small compared to 1. The expression relating the degree of dissociation (x) with equilibrium constant kp and total pressure P is
A(2Kp/P)B(2Kp/P)1/3C(2Kp/P)1/2D(Kp/P)
The dissociation equilibrium of a gas AB2 can be represented as, 2AB2(g)⇔2AB(g)+B2(g). The degree of disssociation is 'x' and is small compared to 1. The expression relating the degree of dissociation (x) with equilibrium constant kp and total pressure P is
View SolutionThe dissociation of a gas AB2 at equilibrium can be represented as :
2AB2(g)⇔2AB(g)+B2(g)
The degree of dissociation is x and is small compared to I. The expression relating the degree of dissociation (x) with equilibrium constant Kp and total pressure P is :
View SolutionThe dissociation equilibrium of a gas AB2 can be represented as, 2AB2(g)⇔2AB(g)+B2(g). The degree of dissociation is x and is small compared to 1. The expression relating the degree of dissociation (x) with equilibrium constant kp and total pressure P is :
View SolutionThe dissociation equilibrium of a gas AB2 can be represented as :
2AB2⇔2AB(g)+B2(g)
The degree of dissocaition x is very small as compared to 1. The expression which relates the degree of dissociation (x) with equilibrium constant (Kp) and total pressure (p) is :
View SolutionThe equilibrium constant (Kp) for the decomposition of gaseous H2O
H2O(g)⇔H2(g)+12O2(g)
is related to the degree of dissociation α at a total pressure P by
View Solution
