A salesperson whose annual earnings can be represented by the function A (x) = 30,000+0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25,000 +0.05 x. Find (A+S) (x) and determine the total family income if they each sell Rs 1,50,00,000 worth of merchandise.Solution in Tamil
The correct Answer is:1,40,5000
Step by step video, text & image solution for A salesperson whose annual earnings can be represented by the function A (x) = 30,000+0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25,000 +0.05 x. Find (A+S) (x) and determine the total family income if they each sell Rs 1,50,00,000 worth of merchandise. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - FULL MARKSCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - Exercise -1.44videos
SETS, RELATIONS AND FUNCTIONS
- BOOK - FULL MARKSCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - Exercise -1.525videos
SETS, RELATIONS AND FUNCTIONS
- BOOK - FULL MARKSCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - Exercise -1.27videos
SETS, RELATIONS AND FUNCTIONS
- BOOK - FULL MARKSCHAPTER - SAMPLEPAPER - 15 (UNSOLVED)EXERCISE - Part - IV (IV. Answer all the questions.)7videos
SAMPLEPAPER - 15 (UNSOLVED)
- BOOK - FULL MARKSCHAPTER - SOLVED PAPER 10EXERCISE - PART-IV8videos
SOLVED PAPER 10
Similar Questions
Graph the functions f (x) = x3 and g(x) = 3√x on the same co-ordinate plane. Find fog and graph it on the plane as well. Explain your results.
03:00View SolutionIf A= {(x,y) : y = ex,x∈R} and B = { (x,y) : y = e−x,x∈R } then n (A ∩ B ) is
02:50View SolutionLet X = {a, b,c,d}, and R = { (a,a) (b,b) (a,c)}. Write down the minimum number of ordered pairs to be included to R to make it
(i) reflexive (ii) symmetric
(iii) transitive (iv) equivalence.03:14View SolutionIf αandβ are the roots of the quadratic equation x2+√2x+3=0 form a quadratic equation with roots1αand1β
06:45View SolutionGraph the functions f(x)=x3andg(x)=3√x on the same coordinate plane. Find f o g and graph it on the plane as well. Explain your results.
03:28View SolutionManufacturer can sell x items at a price of rupees (5−x100)each. The cost price of x items is Rs (x5+500). Find the number of items he should sell to earn maximum profit
03:56View SolutionA manufacturer can sell x items at a price of Rs. (5−x100) each. The cost price of x items is Rs. (x5+ 500). Find the number of items he should sell to earn maximum profit.
04:35View SolutionA salesperson whose annual earnings can be represented by the function A (x) = 30,000+0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25,000 +0.05 x. Find (A+S) (x) and determine the total family income if they each sell Rs 1,50,00,000 worth of merchandise.
05:35View Solution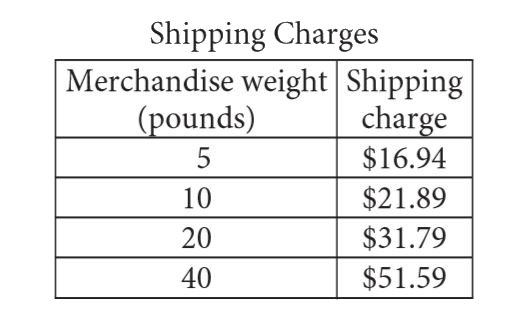
The table above shows shipping charges for an online retailer that sells sporting goods. There is a linear relationship between the shipping charge and the weight of the merchandise. Which function can be used to determine the total shipping charge f (x) , in dollars, for an order with a merchandise weight of x pounds?04:18View SolutionManufacturer can sell x items at a price of Rs. (5−x100) each . The cost price is Rs. (x5+500). Find the number of items he should sell to earn maximum profit.
01:11View Solutionஒரு விற்பனை பிரதிநிதியின் ஆண்டு வருமானத்தைக் குறிக்கும் சார்பு A(x)=30000+0.04x.இங்கு xஎன்பது அவர் விற்கும் பொருளின் விலைமதிப்பை ரூபாயகக் குறிக்கின்றது. விற்பனைத் துறையில் உள்ள அவர் மகனின் வருமானம் S(x)=25,000+0.05xஎனும் சார்பாகக் குறிக்கப்படுகிறது எனில்,(A+S)(x) காண்க. மேலும் 1,50,00,000மதிப்புள்ள பொருட்களை அவர்களிருவரும் தனித்தனியே விற்றால் வருமானம்
01:21View SolutionManufacturer can sell x items at a price of rupees (5−x100) each. Thecost price of x items is Rs (x5+500) . Find the number of items he should sell to earn maximum profit.
03:14View SolutionManufacturer can sell x items at a price of rupees (5−x100) each. Thecost price of x items is Rs (x5+500) . Find the number of items he should sell to earn maximum profit.
03:44View SolutionManufacturer can sell x items at a price of rupees (5−x100) each. The cost price of x items is Rs. (x5+500). Find the number of items he should sell to earn maximum prodit.
05:35View Solutionਕਿਸੇ ਉਤਪਾਦ ਦੀਆਂ x ਇਕਾਈਆਂ ਦੇ ਵੇਚਣ ਤੇ ਪ੍ਰਾਪਤ ਕੁੱਲ ਆਮਦਨ R(x) ਰੁਪਏ ਵਿੱਚ R(x)=13x2+26x+15 ਨਾਲ ਦਰਸਾਈ ਗਈ ਹੈ। ਸੀਮਾਂਤ ਆਮਦਨ ਪਤਾ ਕਰੋ ਜਦੋਂ x = 7 ਹੈ।
08:21View Solutionਇੱਕ ਉਤਪਾਦ ਦੀਆਂ x ਇਕਾਈਆਂ ਦੇ ਵੇਚਣ ਨਾਲ ਪ੍ਰਾਪਤ ਕੁੱਲ ਆਮਦਨ ਰੁਪਏ ਵਿੱਚ R(x)=3x2+36x+5 ਨਾਲ ਦਰਸਾਈ ਗਈ ਹੈ। ਜਦੋਂ x = 15 ਹੈ ਦਾਂ ਸੀਮਾਂਤ ਆਮਦਨ ਹੈ :
08:21View Solution

