Statement 1: ∑0≤i≤j∑≤nC(n,i)C(n,j)=22n−C(2n,n) Statement 2: (n∑r=0)C(n,r))2=n∑r=0(C(n,r))2+2∑0≤i≤j∑≤nC(n,i)C(n,j)
Step by step video & image solution for Statement 1: sum_(0 leqileqj) sum_( leqn) C(n,i) C(n,j)= 2^(2n)-C(2n,n) Statement 2: (sum_(r=0)^n) C(n,r))^2= sum_(r=0)^n (C(n,r))^2+2sum_(0 leqi leqj) sum_(leqn) C(n,i) C(n,j) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Statement -1: n∑r=0r(nCr)2=n(2n−1Cn−1)
Statement-2: n∑r=0(nCr)2=2nCnA1B2C3D4Stetemet - 1: n∑r=0r.nCr=n2n−1
Statement-2: n∑r=0r.nCrxr=n(1+x)n−1xA1B2C3D4Statement-1: n∑r=0(r+1)nCr=(n+2)2n−1
Statement -2: n∑r=0(r+1)nCrxr=(1+x)n+nx(1+x)n−1A1B2C3D4
If n∑r=02rC(n,r)=n∑r=0n3−3n+3C(n,r) then
View SolutionStetemet - 1: n∑r=0r.nCr=n2n−1
Statement-2: n∑r=0r.nCrxr=n(1+x)n−1x
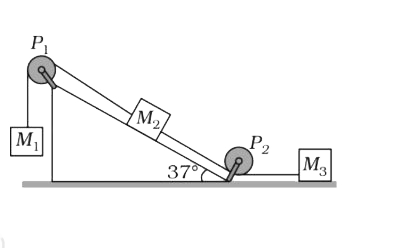
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View SolutionStatement-1: n∑r=0(r+1)nCr=(n+2)2n−1
Statement -2: n∑r=0(r+1)nCrxr=(1+x)n+nx(1+x)n−1
View SolutionProve that n∑r=0r(n−r)Cr2=n2(^(2n−2)Cn).
View Solution
