In a Mathematics examination the numbers scored by 5 candidates are 5 successive odd integers . If their total marks is 185, the highest score is
39
43
41
37
The correct Answer is:C
To solve the problem, we need to find the highest score among 5 candidates who scored 5 successive odd integers that sum up to 185.
1. Define the Variables:
Let the smallest odd integer be represented as x. The five successive odd integers can then be expressed as:
- First integer: x
- Second integer: x+2
- Third integer: x+4
- Fourth integer: x+6
- Fifth integer: x+8
2. Set Up the Equation:
The total of these five integers is given as 185. Therefore, we can set up the equation:
x+(x+2)+(x+4)+(x+6)+(x+8)=185
3. Combine Like Terms:
Simplifying the left side of the equation:
x+x+2+x+4+x+6+x+8=185
This simplifies to:
5x+20=185
4. Solve for x:
To isolate x, subtract 20 from both sides:
5x=185−20
5x=165
Now, divide both sides by 5:
x=1655=33
5. Find the Highest Score:
The highest score among the five integers is:
x+8=33+8=41
Final Answer:
The highest score is 41.
---
Let the smallest odd integer be represented as x. The five successive odd integers can then be expressed as:
- First integer: x
- Second integer: x+2
- Third integer: x+4
- Fourth integer: x+6
- Fifth integer: x+8
The total of these five integers is given as 185. Therefore, we can set up the equation:
x+(x+2)+(x+4)+(x+6)+(x+8)=185
Simplifying the left side of the equation:
x+x+2+x+4+x+6+x+8=185
This simplifies to:
5x+20=185
To isolate x, subtract 20 from both sides:
5x=185−20
5x=165
Now, divide both sides by 5:
x=1655=33
The highest score among the five integers is:
x+8=33+8=41
The highest score is 41.
Similar Questions
In a Mathematics examination the number scored by 5 candidates are 5, successive odd integers. If their total marks are 185, the highest score is a. 39 b. 41 c. 43 d. 47
View SolutionThe pie chart given shows the number of marks scored by a student in the given 5 subjects. The total marks scored by the student is 480.
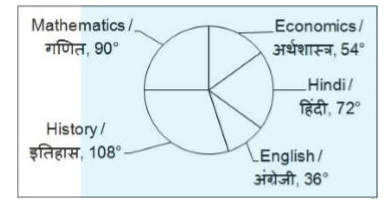
The marks scored by the student in Hindi is how much percent more than the marks scored in Economics?
View Solution
Knowledge Check
In a class of 45 students the ratio of the number of boys and girls is 4:5 The average score of boys in mathematics is 78 .If the average score of all the students in the class in mathematics is 76 , then what is the average score of girls in mathematics ?
A73.6B71.8C72.4D74.4In a class of 45 students, the ratio of the number of boys and girls is 4:5. The average score of boys in mathematics is 78. If the average score of all the students in the class in mathematics is 76, then what is the average score of girls in mathematics?
A73.6B71.8C72.4D74.4
The pie chart given shows the number of marks scored by a student in the given 5 subjects. The total marks scored by the student is 480.
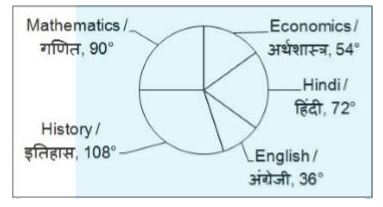
What is the difference between the marks scored by the student in Mathematics and the marks scored in Hindi?
View SolutionThe pie chart given shows the number of marks scored by a student in the given 5 subjects. The total marks scored by the student is 480.
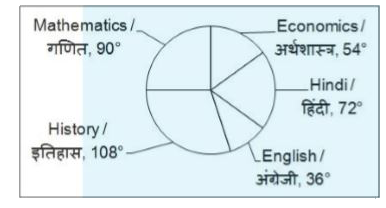
What is the average marks scored by the student in Hindi and Mathematics?
View SolutionThe pie chart given shows the number of marks scored by a student in the given 5 subjects. The total marks scored by the student is 480.
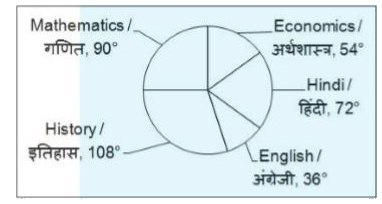
In which of the following 2 subjects the sum of marks scored by the student is equal to the marks scored in Mathematics?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
What percentage of marks the candidate had scored in the subject S5 over the maximum marks of that subject?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
What was the average of marks obtained by the candidate in the subject S5 and S6 together?
View Solution
Who has scored the highest total marks in the all the subjects together ?
View Solution
