If the probability density function of a random variable X is f(x)=x2 in 0≤x≤2, then P(X>1.5∣X>1) is equal to
716
34
712
2164
The correct Answer is:C
Step by step video, text & image solution for If the probability density function of a random variable X is f(x)=x/2 in 0 le x le 2, then P(X gt 1.5 | X gt 1) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - PROBABILITY -2EXERCISE - EXERCISE - 2 : CONCEPT APPLICATOR30videos
PROBABILITY -2
- BOOK - DISHA PUBLICATIONCHAPTER - PROBABILITY -2EXERCISE - EXERCISE - 2 : CONCEPT APPLICATOR30videos
PROBABILITY -2
- BOOK - DISHA PUBLICATIONCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise-2 Concept Applicator20videos
PRINCIPLE OF MATHEMATICAL INDUCTION
- BOOK - DISHA PUBLICATIONCHAPTER - PROBABILITY-1EXERCISE - EXERCISE-1 : CONCEPT BUILDER180videos
PROBABILITY-1
Similar Questions
Knowledge Check
- Question 1 - Select One
If the probability density function of a random variable X is f(x)=π2 in 0≤x≤2, then P(X>1.5X>1) is equal to
A716B34C712D2164 - Question 2 - Select One
If the p.d.f of a random variable X is
F(x)={0.5x0≤x≤20otherwise
Then the value of P(0.5≤X≤1.5) isA14B12C34D1 - Question 3 - Select One
If f(x)={|x|x≤12−xx>1, then fof (x) is equal to
Af(x)=⎧⎪⎨⎪⎩2−xx<−1|x|−1≤x≤1|2−x|x>1Bf(x)=⎧⎪⎨⎪⎩|x|x<−12−|x|−1≤x≤1|2−x|x>1Cf(x)=⎧⎪⎨⎪⎩|2−x|x<−1|x|−1≤x≤12−|x|x>1DNone of these
The probability of a random variable X is given below
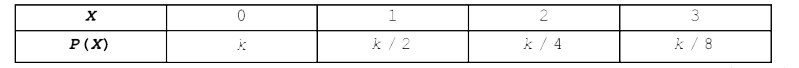
Find P(X≤2)+P(X>2)View SolutionShow that the function f(x) defined by .f(x)=17, for 1≤x≤8 =0, otherwise, is a probability density function for a random variable. Hence find P(3<X<10)
View SolutionThe p.d.f of continuous random variable X is given by f(x)=x8,0<x<4=0 otherwise. Find (i) P(X<2)(ii)P(2<X≤3)(iii)P(X>3.)
View Solutionf(x)={3x−8ifx≤52kifx>5 at x=5
View SolutionIf f(x)=x for x≤0=0 for x>0, then f(x) at x=0 is
View Solution



