A potential barrier of 0.3 V exists across a p-n junction. An electron with speed 5×105 m/s approaches this p-n junction from n-side, what will be its speed on entering the p-side?
3×105m/s
3.8×105m/s
5×105m/s
2.6×103m/s
The correct Answer is:B
To solve the problem, we need to determine the speed of an electron as it crosses a potential barrier of 0.3 V at a p-n junction. The initial speed of the electron is given as 5×105m/s.
1. Understanding the Potential Barrier:
The potential barrier of 0.3 V means that the electron will lose some kinetic energy as it crosses this barrier. The energy lost can be calculated using the formula:
Energy lost=e⋅V
where e is the charge of the electron (1.6×10−19C) and V is the potential barrier (0.3 V).
2. Calculating the Energy Lost:
Energy lost=(1.6×10−19C)⋅(0.3V)=4.8×10−20J
3. Calculating the Initial Kinetic Energy:
The initial kinetic energy (KEi) of the electron can be calculated using the formula:
KEi=12mv2
where m is the mass of the electron (9.11×10−31kg) and v is the initial speed (5×105m/s).
KEi=12(9.11×10−31kg)(5×105m/s)2
KEi=12(9.11×10−31)(2.5×1011)=1.14×10−19J
4. Calculating the Final Kinetic Energy:
The final kinetic energy (KEf) after crossing the barrier will be:
KEf=KEi−Energy lost
KEf=(1.14×10−19J)−(4.8×10−20J)=6.56×10−20J
5. Finding the Final Speed:
Now we can find the final speed (vf) using the final kinetic energy:
KEf=12mv2f
Rearranging gives:
vf=√2⋅KEfm
Substituting the values:
vf=√2⋅(6.56×10−20)9.11×10−31
vf=√1.312×10−199.11×10−31≈√1.44×1011≈1.2×105m/s
Final Answer:
The speed of the electron on entering the p-side is approximately 1.2×105m/s.
The potential barrier of 0.3 V means that the electron will lose some kinetic energy as it crosses this barrier. The energy lost can be calculated using the formula:
Energy lost=e⋅V
where e is the charge of the electron (1.6×10−19C) and V is the potential barrier (0.3 V).
Energy lost=(1.6×10−19C)⋅(0.3V)=4.8×10−20J
The initial kinetic energy (KEi) of the electron can be calculated using the formula:
KEi=12mv2
where m is the mass of the electron (9.11×10−31kg) and v is the initial speed (5×105m/s).
KEi=12(9.11×10−31kg)(5×105m/s)2
KEi=12(9.11×10−31)(2.5×1011)=1.14×10−19J
The final kinetic energy (KEf) after crossing the barrier will be:
KEf=KEi−Energy lost
KEf=(1.14×10−19J)−(4.8×10−20J)=6.56×10−20J
Now we can find the final speed (vf) using the final kinetic energy:
KEf=12mv2f
Rearranging gives:
vf=√2⋅KEfm
Substituting the values:
vf=√2⋅(6.56×10−20)9.11×10−31
vf=√1.312×10−199.11×10−31≈√1.44×1011≈1.2×105m/s
The speed of the electron on entering the p-side is approximately 1.2×105m/s.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR25videos
SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR25videos
SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - DISHA PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise -2 : Concept Applicator26videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR28videos
SYSTEM OF PARTICLES & ROTATIONAL MOTION
Similar Questions
A potential barrier of 0.3V exists across a p−n junction.
(a) if the depletion region is 1μm width. What is the intensity of elctric field in this region ?
(b) An electron with speed 5×105m/sec approaches this p−n junction from n-side, what will be its speed on entering the p-side?View SolutionA potential barrier of 0.50V exists across a p-n junction.(a) If the depletion region is 5.0×10−7m wide,what is the intensity of the electric field in this region?(b) An electron with speed5.0×105ms−1approaches the p-n junction form the n-side.With what speed will it enter the p-side?
View Solution
Knowledge Check
- Question 1 - Select One
When a p-type semiconductor is brought into a close contact with n-type semiconductor, we get a p-n junction with a barrier potential 0.4V and the width of depletion region is 4.0×10−7m. this p-n junction is forwaed biased with a battery of voltage 3V adn negligible internal resistance, in series with a resistance of resistance R, ideal milliammeter with reading 20 mA and key K as shown in Fig.
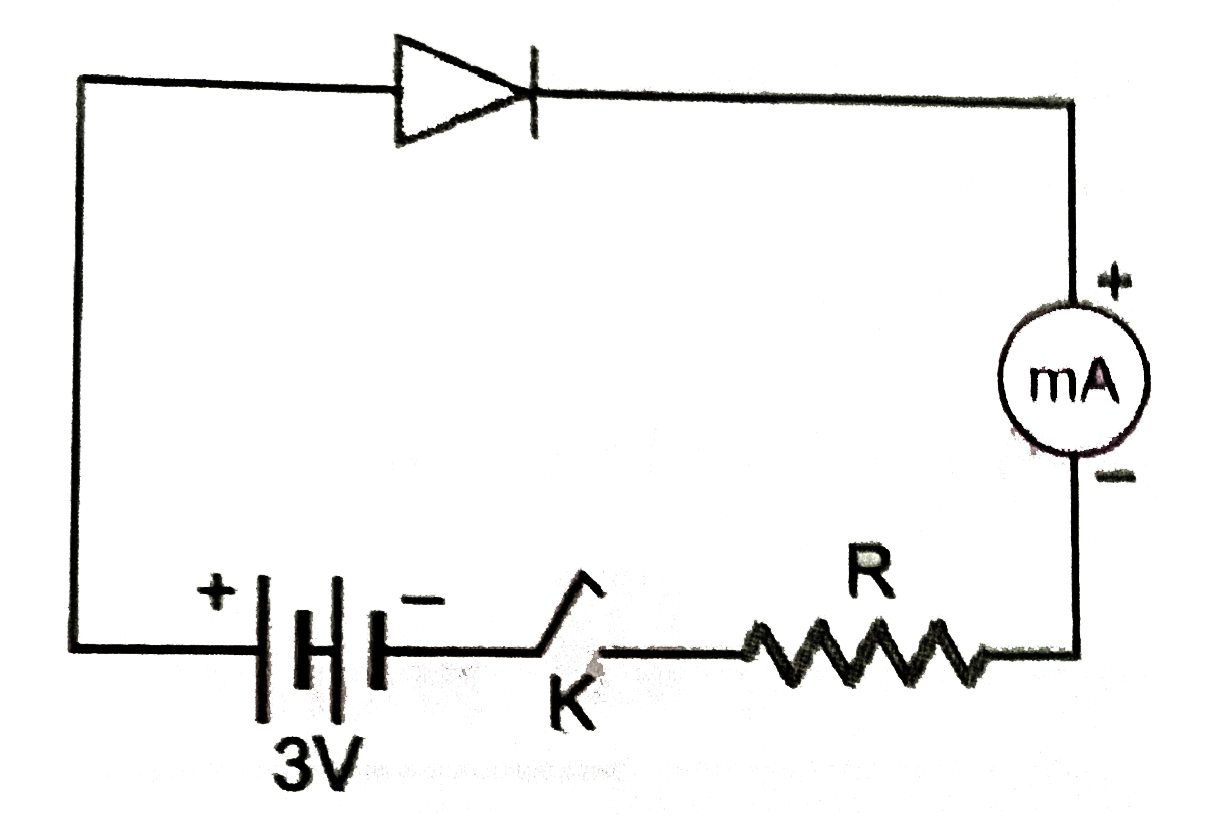
The resistance of resistor R isA1.39×105ms−1B2.78×105ms−1C1.39×106ms−1D2.78×106ms−1 - Question 2 - Select One
A potential barrier of 0.5 V exists across a p-n junction. If the depletion region is 0.5 um wide, the strength of the electric field in the region is
A1.0×106Vm−1B1.0×10−5Vm−1C2.0×105Vm−1D2.0×106Vm−1 - Question 3 - Select One
A potential barrier of 0.3 V exists across a p-n junction. If the depletion region is 1 μm wide, what is the intensity of electric field in this region?
A2×105Vm−1B3×105Vm−1C4×105Vm−1D5×105Vm−1
A potential barrier of 0.60V exixts across a p-n junction. If the depletion region is 6.0×10−7m wide, what is the intensity of the electric field in this region. An electrin with speed 5.0×105ms−1 approaches the p-n junction from the n-side, with what speed will it enter p-side.
View SolutionA potential barrier of 0.4V exists across a p-n junction. If the depletion region is 4.0×10−7m wide, what is the intensity of the electric field in this region? If an electron with speed 4.5×105m/s approaches the p-n junction from the n-side, find the speed with which it will enter the p-side.
View SolutionA potential barrier of 0.3 V exists across a p-n junction. If the depletion region is 1 μm wide, what is the intensity of electric field in this region?
View SolutionIf an electron approaches the p-n junction from the n-side with a speed of 5×105ms−1 ,with what speed will it enter the p-side?
View SolutionA potential barrier of 0.5V exists across a p-n junction . If the widht of depletion layer is 10−6m, then intensity of electric field in this region will be
View Solution

