The period of revolution(T) of a planet moving round the sun in a circular orbit depends upon the radius (r) of the orbit, mass (M) of the sun and the gravitation constant (G). Then T is proportioni of ra. The value of a is
To solve the problem of finding the value of a in the relationship between the period of revolution T of a planet and the radius r of its orbit, as well as the mass M of the sun and the gravitational constant G, we will use dimensional analysis.
1. Establish the relationship:
We assume that the period T is proportional to ra, Mb, and Gc. Thus, we can write:
T∝raMbGc
2. Identify the dimensions:
- The dimension of time T is (T).
- The dimension of radius r is (L).
- The dimension of mass M is (M).
- The gravitational constant G has the dimensions (G)=(M−1L3T−2).
3. Write the dimensional equation:
From the relationship, we can express the dimensions as:
(T)=(L)a(M)b(G)c
Substituting the dimensions of G:
(T)=(L)a(M)b(M−1L3T−2)c
This expands to:
(T)=(L)a(M)b(M−cL3cT−2c)
Rearranging gives:
(T)=(L)a+3c(M)b−c(T)−2c
4. Equate dimensions:
For the dimensions to be equal, we must have:
- For (T): −2c=1 (since the dimension of T on the left side is (T)1)
- For (M): b−c=0
- For (L): a+3c=0
5. Solve the equations:
- From −2c=1, we find:
c=−12
- Substituting c into b−c=0:
b+12=0⟹b=−12
- Now substituting c into a+3c=0:
a+3(−12)=0⟹a−32=0⟹a=32
6. Conclusion:
The value of a is:
32
We assume that the period T is proportional to ra, Mb, and Gc. Thus, we can write:
T∝raMbGc
- The dimension of time T is (T).
- The dimension of radius r is (L).
- The dimension of mass M is (M).
- The gravitational constant G has the dimensions (G)=(M−1L3T−2).
From the relationship, we can express the dimensions as:
(T)=(L)a(M)b(G)c
Substituting the dimensions of G:
(T)=(L)a(M)b(M−1L3T−2)c
This expands to:
(T)=(L)a(M)b(M−cL3cT−2c)
Rearranging gives:
(T)=(L)a+3c(M)b−c(T)−2c
For the dimensions to be equal, we must have:
- For (T): −2c=1 (since the dimension of T on the left side is (T)1)
- For (M): b−c=0
- For (L): a+3c=0
- From −2c=1, we find:
c=−12
- Substituting c into b−c=0:
b+12=0⟹b=−12
- Now substituting c into a+3c=0:
a+3(−12)=0⟹a−32=0⟹a=32
The value of a is:
32
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -2 (Motion in a Straight Line)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -3 (MOTION IN PLANE)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR30videos
ATOMS
- BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator30videos
COMMUNICATION SYSTEM
Similar Questions
The period of revolution (T) of a planet around the sun depends upon (i) radius (r ) of obit (ii) mass M of the sun and (iii) gravi-tational constant G. Prove that T2∝r3
View SolutionConsider a planet of mass (m), revolving round the sun. The time period (T) of revolution of the planet depends upon the radius of the orbit (r), mass of the sun (M) and the gravitational constant (G). Using dimensional analysis, verify Kepler' third law of planetary motion.
View Solution
Knowledge Check
- Question 1 - Select One
If a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
A4π2r3/GTB4π2r3/GT2C4π2r/GTD4π2r3/G2T2 - Question 2 - Select One
The period of revolution of a planet about the sun is T. If a is radius of the circular orbit, then what is true?
ATαaBTαa2CT2αa3DT3αa2 - Question 3 - Select One
If T be the period of revolution of a plant revolving around sun in an orbit of mean radius R, then identify the incorrect graph.
A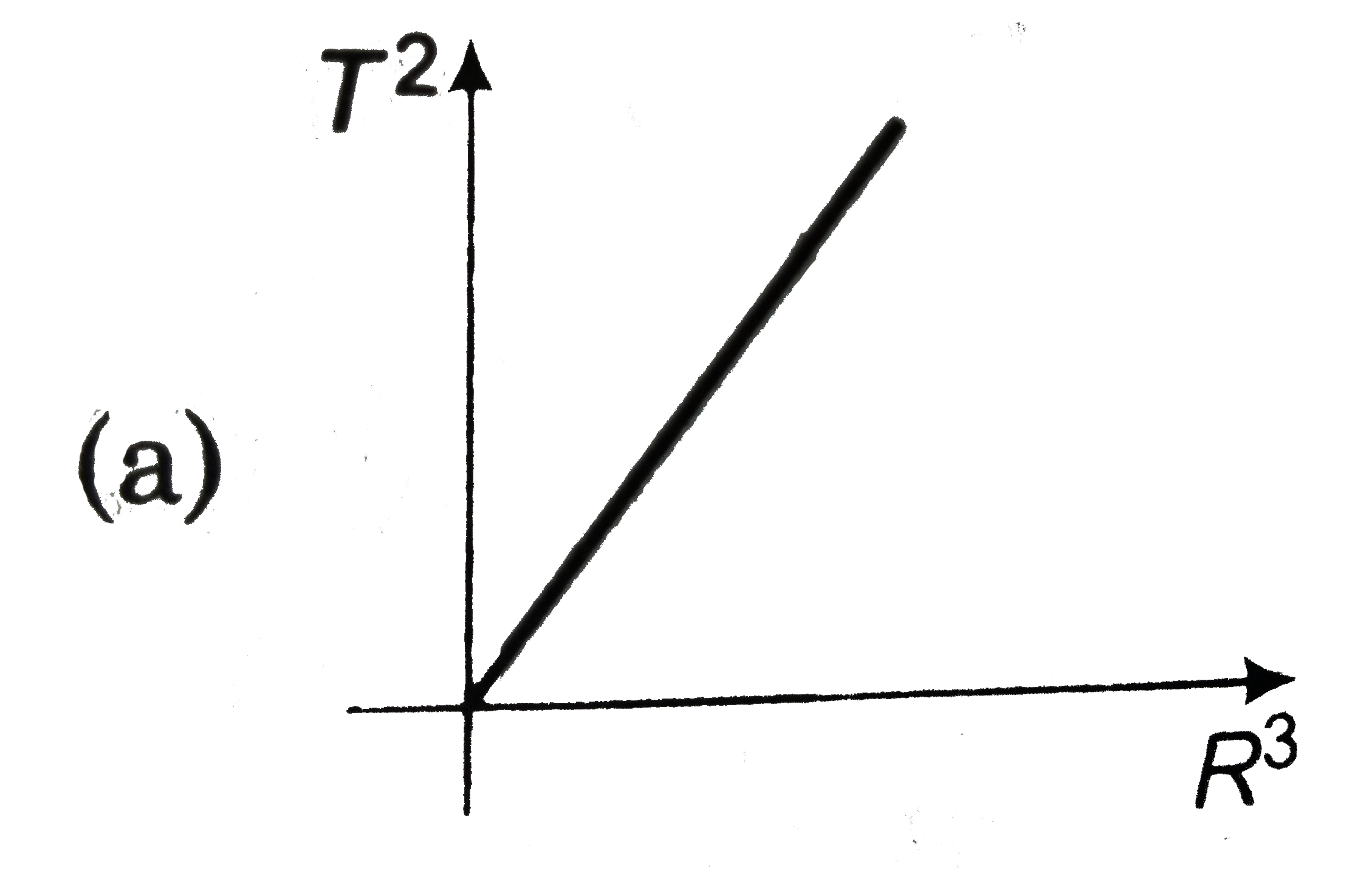 B
B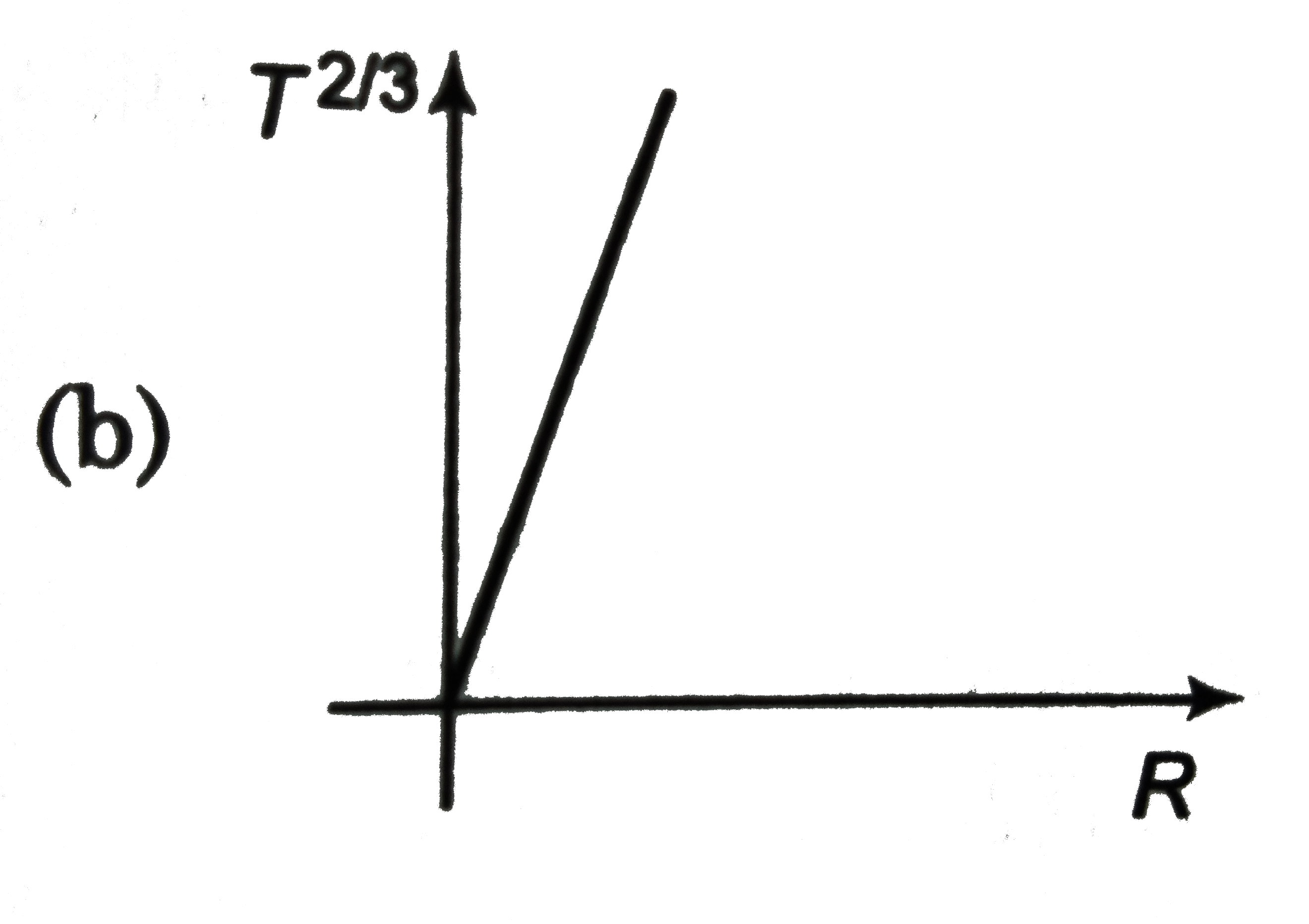 C
C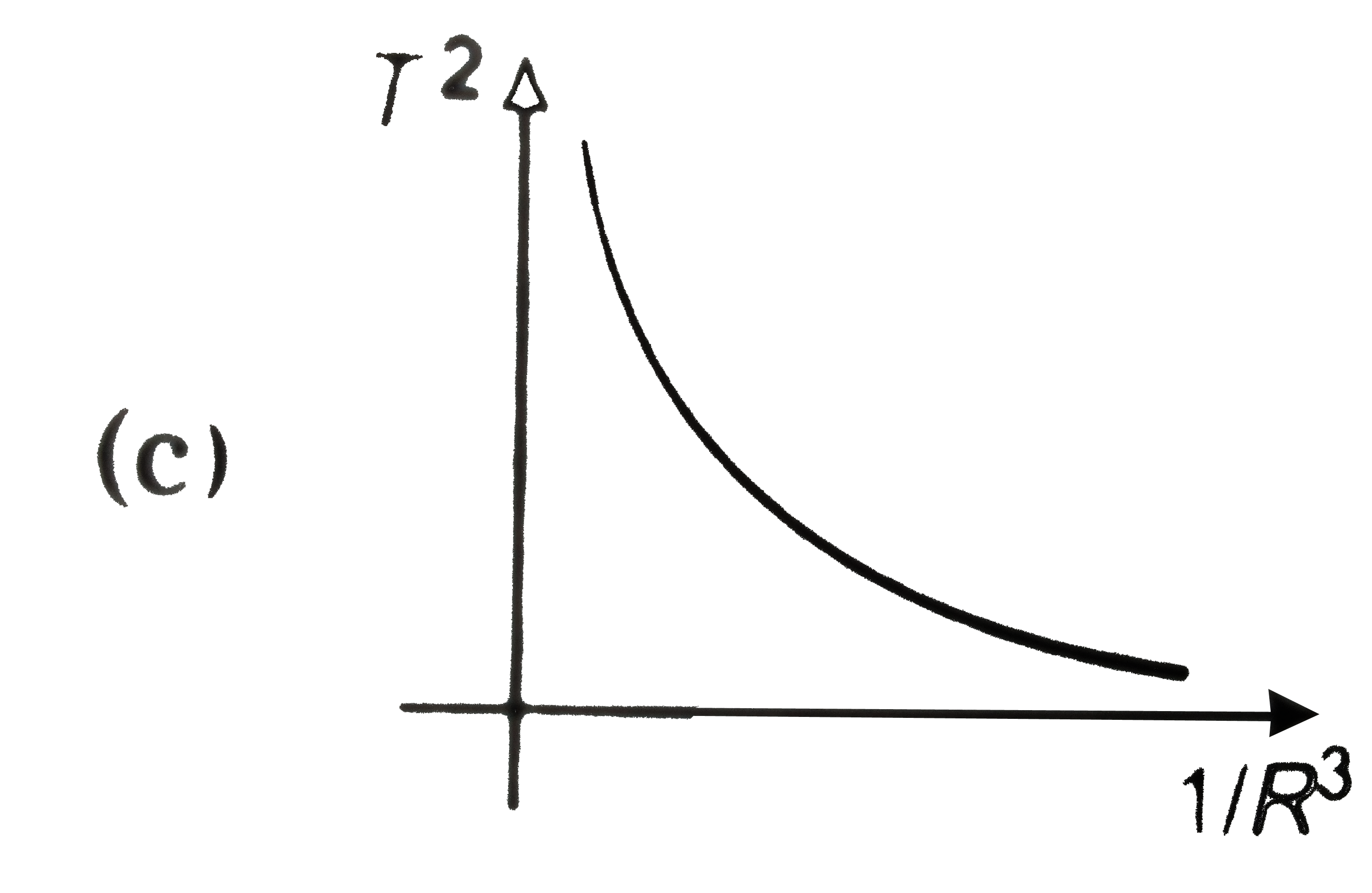 DNone of these
DNone of these
A planet moves around the sun in nearly circular orbit. Its period of revolution 'T' depends upon :
(i) radius 'r' or orbit (ii) mass 'M' of the sum and
(iii) the gravitational constant G.
Show dimensionally that T2∝r2.View SolutionFor a planet of mass M, moving around the sun in an orbit of radius r, time period T depends on its radius (r ), mass M and universal gravitational constant G and can be written as : T2=KryMG. Find the value of y.
View SolutionThe period of revolution of a planet around the sun in a circular orbit is T. If a similar planet is revolving in a circular orbit of the same radius around the sun with its mass twice as that of planet, its period of revolution would be
View SolutionA planet is revolving around the sun in a circular orbit with a radius r. The time period is T .If the force between the planet and star is proportional to r−3/2 then the quare of time period is proportional to
View SolutionA planet is revolving around a star in a circular orbit of radius R with a period T. If the gravitational force between the planet and the star is proportional to R−3/2, then
View Solution

