The coefficient of cubical expansion of mercury is 0.00018/∘C and that of brass 0.00006/∘C. If a barometer having a brass scale were to read 74.5 cm at 30∘C find the true barometric height (in cm) at 0∘C. Tlhe scale is supposed tobe correct at 15∘C.
To find the true barometric height at 0∘C when a barometer reads 74.5 cm at 30∘C using a brass scale, we will follow these steps:
Step 1: Determine the Coefficient of Linear Expansion of Brass
The coefficient of cubical expansion (γ) of brass is given as 0.00006∘C−1. We can find the coefficient of linear expansion (α) using the relationship:
α=γ3
Substituting the value of γ:
αbrass=0.000063=0.00002∘C−1
Step 2: Calculate the Change in Length of the Brass Scale
The scale is correct at 15∘C, and we need to find the change in length when the temperature changes from 15∘C to 30∘C. The change in temperature (ΔT) is:
ΔT=30−15=15∘C
The change in length (ΔL) can be calculated using the formula:
ΔL=L⋅α⋅ΔT
Where L is the observed length (74.5 cm):
ΔL=74.5⋅0.00002⋅15
Calculating ΔL:
ΔL=74.5⋅0.00002⋅15=0.02235cm
Step 3: Calculate the True Length at 30∘C
The true length at 30∘C is the observed length plus the change in length:
L30=L+ΔL=74.5+0.02235=74.52235cm
Step 4: Relate the Densities of Mercury at Different Temperatures
The density of mercury at 30∘C can be related to its density at 0∘C using the formula for volume expansion:
ρ30=ρ01+γm⋅ΔT
Where γm is the coefficient of cubical expansion of mercury (0.00018∘C−1) and ΔT=30∘C:
ρ30=ρ01+0.00018⋅30
Calculating:
ρ30=ρ01+0.0054=ρ01.0054
Step 5: Use the Barometric Formula to Find True Height at 0∘C
Using the barometric formula, we have:
P0=P30⟹ρ0⋅g⋅H0=ρ30⋅g⋅H30
Since g cancels out, we can write:
H0=ρ30ρ0⋅H30
Substituting ρ30:
H0=(ρ01.0054⋅ρ0)⋅74.52235
This simplifies to:
H0=74.522351.0054
Calculating H0:
H0≈74.122cm
Final Answer
The true barometric height at 0∘C is approximately 74.122cm.
---
The coefficient of cubical expansion (γ) of brass is given as 0.00006∘C−1. We can find the coefficient of linear expansion (α) using the relationship:
α=γ3
Substituting the value of γ:
αbrass=0.000063=0.00002∘C−1
The scale is correct at 15∘C, and we need to find the change in length when the temperature changes from 15∘C to 30∘C. The change in temperature (ΔT) is:
ΔT=30−15=15∘C
The change in length (ΔL) can be calculated using the formula:
ΔL=L⋅α⋅ΔT
Where L is the observed length (74.5 cm):
ΔL=74.5⋅0.00002⋅15
Calculating ΔL:
ΔL=74.5⋅0.00002⋅15=0.02235cm
The true length at 30∘C is the observed length plus the change in length:
L30=L+ΔL=74.5+0.02235=74.52235cm
The density of mercury at 30∘C can be related to its density at 0∘C using the formula for volume expansion:
ρ30=ρ01+γm⋅ΔT
Where γm is the coefficient of cubical expansion of mercury (0.00018∘C−1) and ΔT=30∘C:
ρ30=ρ01+0.00018⋅30
Calculating:
ρ30=ρ01+0.0054=ρ01.0054
Using the barometric formula, we have:
P0=P30⟹ρ0⋅g⋅H0=ρ30⋅g⋅H30
Since g cancels out, we can write:
H0=ρ30ρ0⋅H30
Substituting ρ30:
H0=(ρ01.0054⋅ρ0)⋅74.52235
This simplifies to:
H0=74.522351.0054
Calculating H0:
H0≈74.122cm
The true barometric height at 0∘C is approximately 74.122cm.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 11 (THERMODYNAMICS)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 12 (KINETIC THEORY)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER-9 (MECHANICAL PROPERTIES OF FLUIDS)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR30videos
ATOMS
- BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator30videos
COMMUNICATION SYSTEM
Similar Questions
The coefficient of linear expansion for brass is 0.000018/∘C. Explain the meaning of this statement.
View Solution(a) The brass scale of a barometer gives correct reading at 0∘C . Coefficient of linear expansion of brass is 2.0×10−5/∘C . The barometer reads 75cm at 27∘C . What is the atmospheric pressure at 27∘C ?
(b) A barometer reads 75.0cm on a steel scale. The room temperature is 30∘C . The scale is correctly graduated for 0∘C . The coefficient of linear expansion of steel is α=1.2×10−5/∘C and the coefficient of volume expansion of mercury is γ=1.8×10−4/∘C . Find the correct atmospheric pressure.View Solution
Knowledge Check
- Question 1 - Select One
The Coefficient of cubical expansion of mercury is 0.0018/∘C and that of brass 0.000006/∘C, find the true barmetric height at 0∘C.The scale is supposed to be coreect at 15∘C
A74.122 cmB79.125 cmC42.161cmD142.39 cm - Question 2 - Select One
Coefficient of apparent expansions of mercury is 0.18×10−3/0C. If the density of mercury at 00C is 13.6g/cc its density at 473K will be
A13.12g/c.c.B13.65g/c.c.C13.51g/c.c.D13.22g/c.c. - Question 3 - Select One
The coefficient of volumetric expansion of mercury is 18×10−5/∘C . A thermometer bulb has a volume 10−6m3 and cross section of stem is 0.004cm2. Assuming that bulb is filled with mercury at 0∘C then the length of the mercury column at 100∘C is
A18.8mmB9.2mmC7.4mmD4.5cm
the height of mercury in a fauilty barometer is 75 cm and the tube above mercury is 10 cm long. The correct barometer reading is 76 cm. when the faulty barometer reads 74 cm, find the true barometer reading .
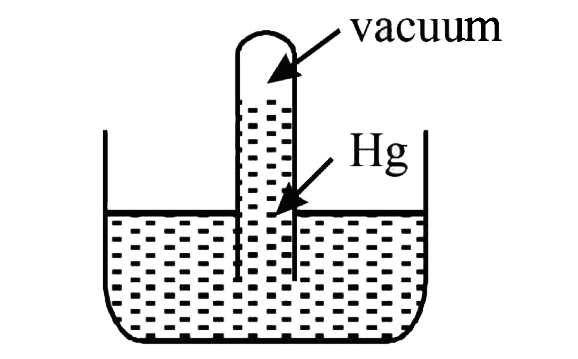
View SolutionA barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018perC∘ and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C, but the temperature of the atmosphere does not raised by 1∘C, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
 View Solution
View SolutionThe correct value of 0∘C on the kelvin scale is
View SolutionThe correct value of 0∘C on the Kelvin scale is
View SolutionThe correct value of 0∘C on the Kelvin scale is
View Solution

