Anvils made of single crystals of diamond, with the shape as shown in Fig. 9.14, are used to investigate behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of 0.50 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil ?
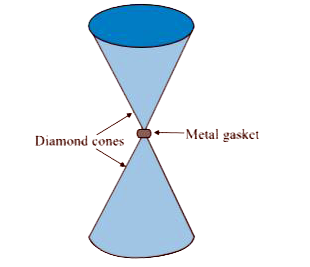
The correct Answer is:Pressure at the tip of anvil is 2.5×1011 Pa
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDS BOOK - NCERT TELUGUCHAPTER - MECHANICAL PROPERTIES OF SOLIDS EXERCISE - Exercises
21 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - NCERT TELUGUCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE
45 Videos
- MOTION IN A PLANEBOOK - NCERT TELUGUCHAPTER - MOTION IN A PLANEEXERCISE - EXCERCISES
30 Videos
Similar Questions
Anvils made of single crystal of diamond , with shape as shown in fig. are used to investigate behaviour of materials under very high pressure. Flat faces at the narrow end of the anvil have a diameter of 0.5 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil?
View SolutionAnvils made of single crystal of diamond , with shape as shown in fig. are used to investigate behaviour of materials under very high pressure. Flat faces at the narrow end of the anvil have a diameter of 0.5 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil?
View Solution
Knowledge Check
Attempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
The force 10−3 N, is equivalent to:
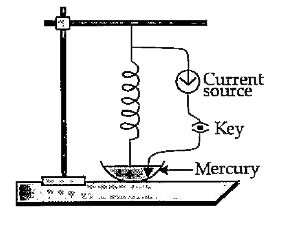A100 mgB100 gC10 gD10 mgAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What else can be used instead of mercury in Roget's spiral?
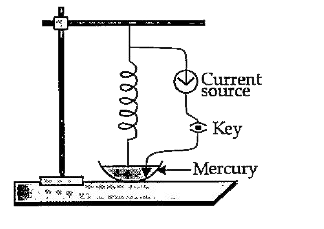AAny liquidBWaterCKerosene oilDOnly mercury, nothing elseAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What are main 3 components in a Roget's spiral?
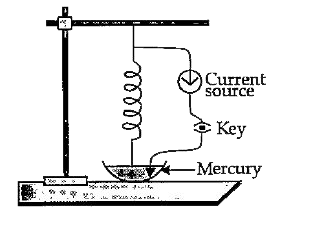AMarcury, AC voltage sourceBMercury, DC voltage sourceCMercury, DC voltage source, keyDMercury, AC voltage source, key
When a sound wave enters the ear, it sets the eardrum into oscillation, which in turn causes oscillation of 3 tiny bones in the middle ear called ossicles. This oscillation is finally transmitted to the fluid filled in inner portion of the ear termed as inner ear, the motion of the fluid disturbs hair cells within the inner ear which transmit nerve impulses to the brain with the information that a sound is present. The theree bones present in the middle ear are named as hammer, anvil and stirrup. Out of these the stirrup is the smallest one and this only connects the middle ear to inner ear as shown in the figure below. The area of stirrup and its extent of connection with the inner ear limits the sensitivity of the human ear consider a person's ear whose moving part of the eardrum has an area of about 50mm2 and the area of stirrup is about 5mm2. The mass of ossicles is negligible. As a result, force exerted by sound wave in air on eardum and ossicles is same as the force exerted by ossicles on the inner ear. Consider a sound wave having maximum pressure fluctuation of 4×10−2Pa from its normal equilibrium pressure value which is equal to 105Pa. Frequency of sound wave in air is 332ms. Velocity of sound wave in fluid (present in inner ear) is 1500ms. Bulk modulus of air is 1.42×105Pa. Bulk modulus of fluid is 2.18×109Pa.
Q. Find the pressure amplitude of given sound wave in the fluid of inner ear.
View Solution
When a sound wave enters the ear, it sets the eardrum into oscillation, which in turn causes oscillation of 3 tiny bones in the middle ear called ossicles. This oscillation is finally transmitted to the fluid filled in inner portion of the ear termed as inner ear, the motion of the fluid disturbs hair cells within the inner ear which transmit nerve impulses to the brain with the information that a sound is present. The theree bones present in the middle ear are named as hammer, anvil and stirrup. Out of these the stirrup is the smallest one and this only connects the middle ear to inner ear as shown in the figure below. The area of stirrup and its extent of connection with the inner ear limits the sensitivity of the human ear consider a person's ear whose moving part of the eardrum has an area of about 50mm2 and the area of stirrup is about 5mm2. The mass of ossicles is negligible. As a result, force exerted by sound wave in air on eardum and ossicles is same as the force exerted by ossicles on the inner ear. Consider a sound wave having maximum pressure fluctuation of 4×10−2Pa from its normal equilibrium pressure value which is equal to 105Pa. Frequency of sound wave in air is 332ms. Velocity of sound wave in fluid (present in inner ear) is 1500ms. Bulk modulus of air is 1.42×105Pa. Bulk modulus of fluid is 2.18×109Pa.
Q. If the person is using an hearing aid, which increase the sound intensity level by 30 dB, then by what factor the intensity of given sound wave change as perceived by inner ear?
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Why the spring shrinks in Roget's spiral?
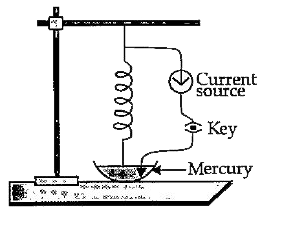
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Magnetic effects:
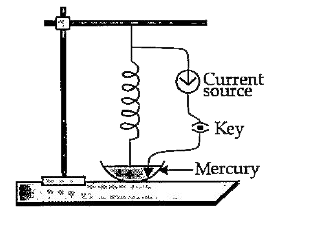
View Solution-
When a sound wave enters the ear, it sets the eardrum into oscillation, which in turn causes oscillation of 3 tiny bones in the middle ear called ossicles. This oscillation is finally transmitted to the fluid filled in inner portion of the ear termed as inner ear, the motion of the fluid disturbs hair cells within the inner ear which transmit nerve impulses to the brain with the information that a sound is present. The theree bones present in the middle ear are named as hammer, anvil and stirrup. Out of these the stirrup is the smallest one and this only connects the middle ear to inner ear as shown in the figure below. The area of stirrup and its extent of connection with the inner ear limits the sensitivity of the human ear consider a person's ear whose moving part of the eardrum has an area of about 50mm2 and the area of stirrup is about 5mm2. The mass of ossicles is negligible. As a result, force exerted by sound wave in air on eardum and ossicles is same as the force exerted by ossicles on the inner ear. Consider a sound wave having maximum pressure fluctuation of 4×10−2Pa from its normal equilibrium pressure value which is equal to 105Pa. Frequency of sound wave in air is 332ms. Velocity of sound wave in fluid (present in inner ear) is 1500ms. Bulk modulus of air is 1.42×105Pa. Bulk modulus of fluid is 2.18×109Pa.
Q. Find the pressure amplitude of given sound wave in the fluid of inner ear.
View Solution