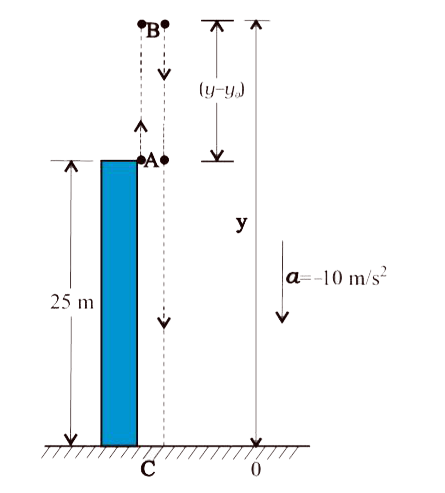
A ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2. Solution in Telugu
(a) Let us take the y-axis in the vertically upward direction with zero at the ground, as shown in Fig.
Now υ0=+20ms−1,
a=−g=−10ms−2,
υ=0ms−1
If the ball rises to height y from the point of launch, then using the equation
υ2=υ20+2(y−y0)
we get
0=(20)2+2(−10)(y−y0)
Solving, we get, (y−y0)=20m.
(b) We can solve this part of the problem in two ways.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NCERT TELUGUChapter:MOTION IN A STRAIGHT LINEExercise:EXERCISES
Explore 23 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT TELUGUChapter:MOTION IN A STRAIGHT LINEExercise:ADDITIONAL EXERCISES
Explore 5 Videos
- MOTION IN A PLANEBook:NCERT TELUGUChapter:MOTION IN A PLANEExercise:EXCERCISES
Explore 30 Videos
- OSCILLATIONSBook:NCERT TELUGUChapter:OSCILLATIONSExercise:Additional Exercises
Explore 6 Videos
Similar Questions
In which of the following examples of motion, can the body be considered approximately a point object:
(a) a railway carriage moving without jerks between two stations.
(b) a monkey sitting on top of a man cycling smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on hitting the ground.
(d) a tumbling beaker that has slipped off the edge of a table.
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
View SolutionState , for each of the following physical quantities , if it is a scalar or a vector : volume , mass , speed , acceleration , density , number of moles , velocity , angular frequency , displacement , angular velocity .
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].

View SolutionA ball is thrown vertically upwards with a velcotiy of 20 ms^(-1) from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25-0m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10 ms^(-2) .
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25 m from the ground. How long will it be before the ball hits the ground (Take, g=10ms−2) ?
View Solution25 मीटर ऊँचे मीनार से एक गेंद 10 मी/से के वेग से ऊर्ध्वाधर ऊपर की ओर फेंकी जाती है।
गेंद धरती से टकराने के पहले कितना समय लेगी ?
(g=10मी/से2)
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multi-storey building. The height of the point from where the boll is thrown is 25.0m from the ground (a) How high will the ball rise? and (b) How long will it take to reach the ground?
View SolutionA ball is thrown vertically upwards with a velocity of 20ms^-1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. How high will the ball rise?
View SolutionA ball is thrown vertically upwards with a velocity of 20ms^-1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. How long will it be before the balls hits the ground? Take g=10ms^-2 [Actual value of g is 9.8ms^-2] .
View SolutionA ball is thrown vertically upwards with a velocity of 20 ms^(-1) from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g = 10 ms^(-2) .
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velcotiy of 20 ms^(-1) from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10 ms^(-2) .
View Solution