Let s be set of all in a plane and let R be a relation on s defined by then ,R is
Reflexive and symmetric but transitive
Reflexive and transitive but not symmetric
symmetric and transitive but not reflexive
An equivalence relation
The correct Answer is:D
Step by step video, text & image solution for Let s be set of all Delta in a plane and let R be a relation on s defined by Delta_(1) S Delta_(2)hArr Delta_(1)-= Delta_(2). then ,R is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - RELATIONSEXERCISE - Exercise 1B13videos
RELATIONS
- BOOK - RS AGGARWALCHAPTER - PRODUCT OF THREE VECTORSEXERCISE - Objective Questions34videos
PRODUCT OF THREE VECTORS
- BOOK - RS AGGARWALCHAPTER - SCALAR, OR DOT, PRODUCT OF VECTORSEXERCISE - Exercise 2334videos
SCALAR, OR DOT, PRODUCT OF VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
Let S be the set of all real number and let R be relation on S , defined by
aRb⇔(1+ab)>0 then, R isAReflexive and symmetric but transitiveBReflexive and transitive but not symmetricCsymmetric and transitive but not reflexiveDNone of these - Question 2 - Select One
Let S be the set of all real numbers and Let R be a relations on s defined by aRB⇔|a|≤b. then ,R is
AReflexive and symmetric but transitiveBsymmetric and transitive but not reflexiveCReflexive and transitive but not symmetricDNone of these - Question 3 - Select One
Let S be set of all numbers and let R be a relation on S defined by aRb⇔a2+b2=1 then, R is
Asymmetric and transitive but not reflexiveBReflexive and symmetric but transitiveCReflexive and transitive but not symmetricDNone of these
Let S be the set of all triangles and R+ be the set of positive real numbers. Then the function f:S→R+,f(Δ)=areaofΔ,where∈S, is injective but not surjective. surjective but not injective injective as well as surjective neither injective nor surjective
View SolutionIf S be the set of all triangles and f:S→R+,f(Δ)= Area of Δ, then f is-
View SolutionLet S be set of all real numbers and let R be relation on S, defined by aRb⇔|a−b|≤1. then R is
View SolutionIf S is the set of all triangles lying in plane and relation R is defined on S as :
R={(S1,S2):S1 is congruent to S2, where S1 and S2 belong to S}View SolutionA substance is carried through the following transformations:
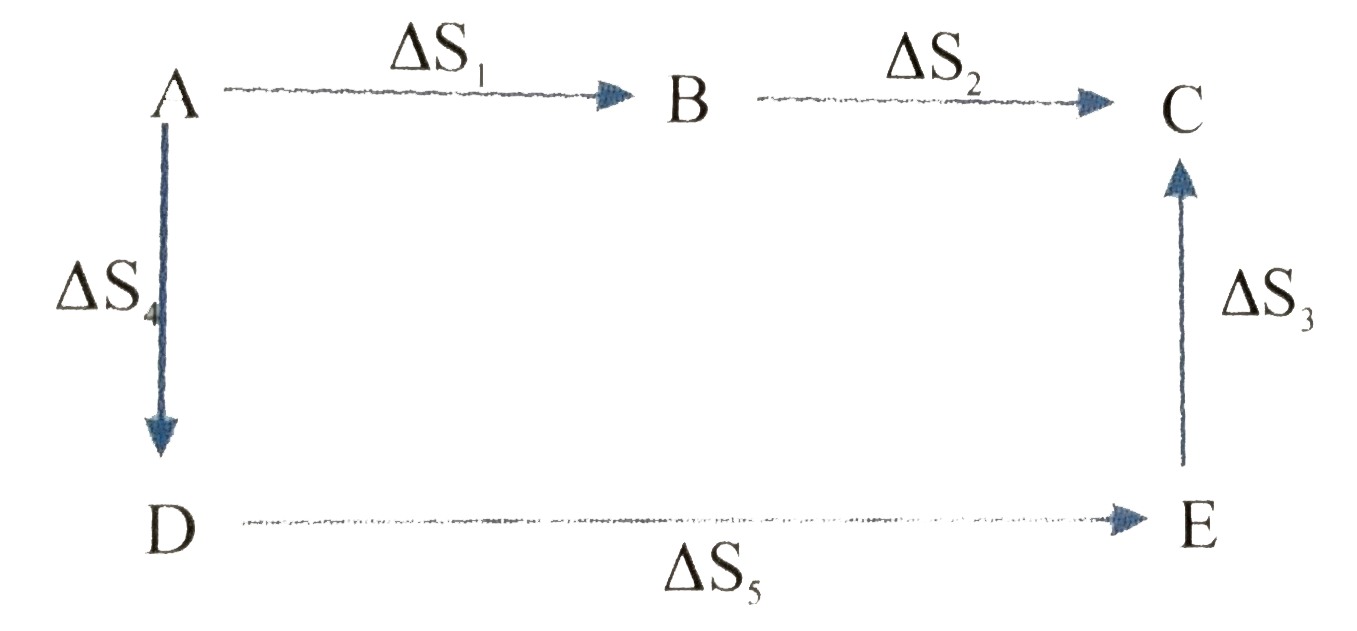
The equation ΔS1+ΔS2=ΔS3+ΔS4+ΔD5View Solution

