Draw the graph of the function $f (x) = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} x^{2}, & when & x < 0 x, & when & 0 \leq x \leq 1 1 / x, & when & 1 \leq x < \infty . \end{matrix}$

Video Solution

Text Solution

Verified by Experts

Here, the graph consists of three parts. Some of the points of the graph are $(- 3, 9), (- 2, 4), (- 1, 1), (0, 0), (\frac{1}{2}, \frac{1}{2}), (\frac{3}{4}, \frac{3}{3}), (1, 1), (2, \frac{1}{2}), (3, \frac{1}{3})$ , etc.
And the graph may now be drawn ,as shown in the adjoining figure.

|

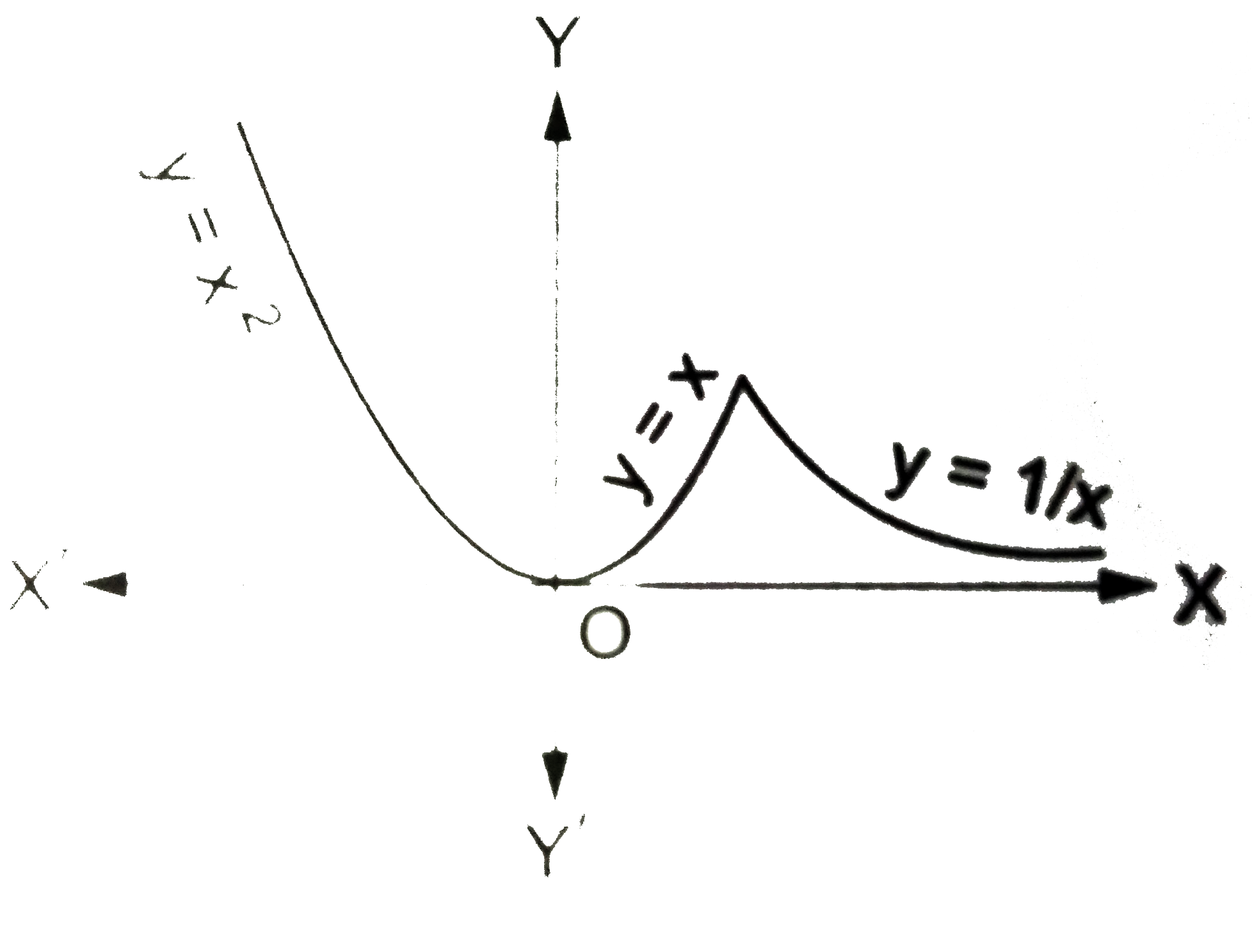
Updated on:21/07/2023

Class 12 MATHS CONTINUITY AND DIFFERENTIABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The function $f (x) = {\begin{matrix} 1 + x, when x \leq 2 5 - x, when x > 2 \end{matrix}$ is
Acontinuous as well as differntiable at x= 2
Bcontinuous but not differntiable at x = 2
Cdifferentiable but not continuous at x = 2
Dnone of these
Question 2 - Select One
If $f (x) = {\begin{matrix} x^{2} & , & when x \leq 1 x + 5 & , & when x = 1 \end{matrix}$ , then
Af(x) is continuous at $x = 1$
Bf(x) is discontinuous at $x = 1$
C $lim x \to 1^{+} f (x) = 1$
D $lim x \to 1^{+} f (x) = 6$
Question 3 - Select One
If $f (x) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} - x^{2}, & w h e n x \leq 0 5 x - 4, & when 0 < x \leq 1 4 x^{2} - 3 x, & when 1 < x < 2 3 x + 4, & w h e n x \geq 2 \end{matrix}$ ,then
Af(x) is continuous at x = 0
Bf(x) is continuous at x = 2
Cf(x) is discontinuous at x = 1
DNone of these

RS AGGARWAL-CONTINUITY AND DIFFERENTIABILITY-Exercise 9C

Home
Ask Doubt
Profile