$f (x) = {[x (x - 3)]}^{2}$ is increasing in

A

$(0, \infty)$

B

$(- \infty, 0)$

C

$(1, 3)$

D

$(0, \frac{3}{2}) \cup (3, \infty)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$f (x) = {[x (x - 3)]}^{2} \Rightarrow f' (x) = 2 x (x - 3) (2 x - 3)$
$∴ f' (x) = 0 \Rightarrow x = 0 or x = \frac{3}{2} or x = 3$
$f (x)$ is increasing when $0 < x < \frac{3}{2} or x > 3$
$∴ f (x)$ is increasing in $(0, \frac{3}{2}) \cup (3, \infty)$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

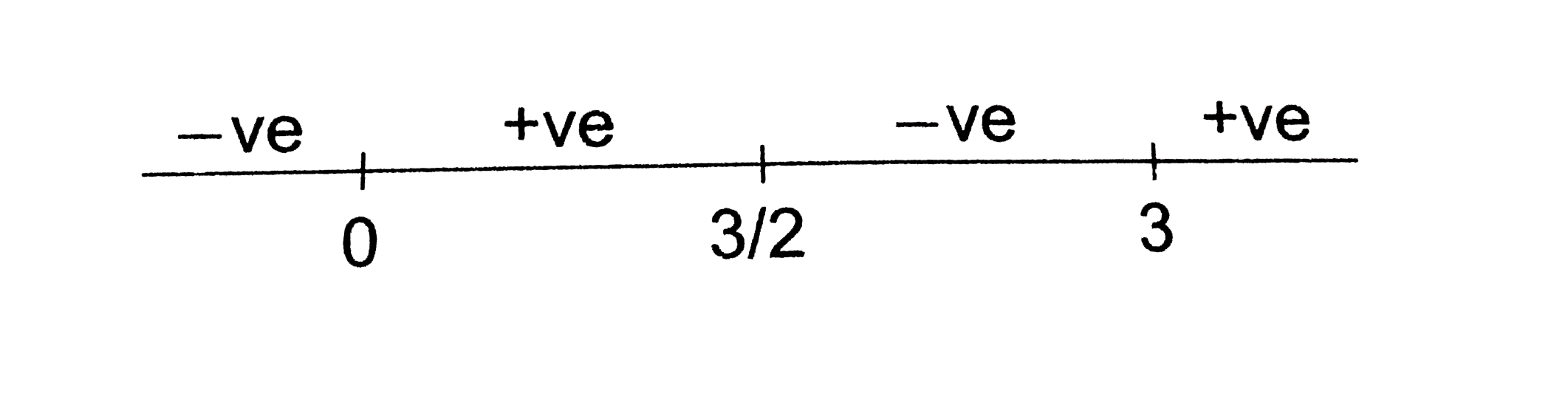
Topper's Solved these Questions

Similar Questions

Knowledge Check

The function f(x)= ${[x (x - 2)]}^{2}$ is increasing in the set
A $(- \infty, 0) \cup (2, \infty)$
B $(- \infty, 1)$
C $(0, 1) \cup (2, \infty)$
D(1,2)
$f (x) = {(x + 1)}^{3} {(x - 3)}^{3}$ is increasing in
A $(- \infty, 1)$
B $(- 1, 3)$
C $(3, \infty)$
D $(1, \infty)$
$f (x) = x^{2} (x - 8)$ is increasing in
A $(- \infty, 0)$
B $(- \infty, 1)$
C $(0, \frac{16}{3})$
DR

RS AGGARWAL-APPLICATIONS OF DERIVATIVES-Objective Questions

Home
Ask Doubt
Profile