Find the coordinates of foot of perpendicular and the length of the perpendicular drawn from the point P(5,4,2) to the line $\to r = (- ˆ i + 3 ˆ j + ˆ k) + λ (2 ˆ i + 3 ˆ j \pm ˆ k)$ Also find the image of p in this line .

Text Solution

Verified by Experts

The vector equation fo the given line is
$\to r = (- ˆ i + 3 ˆ j + ˆ k) + λ (2 ˆ i + 3 ˆ j - ˆ k)$

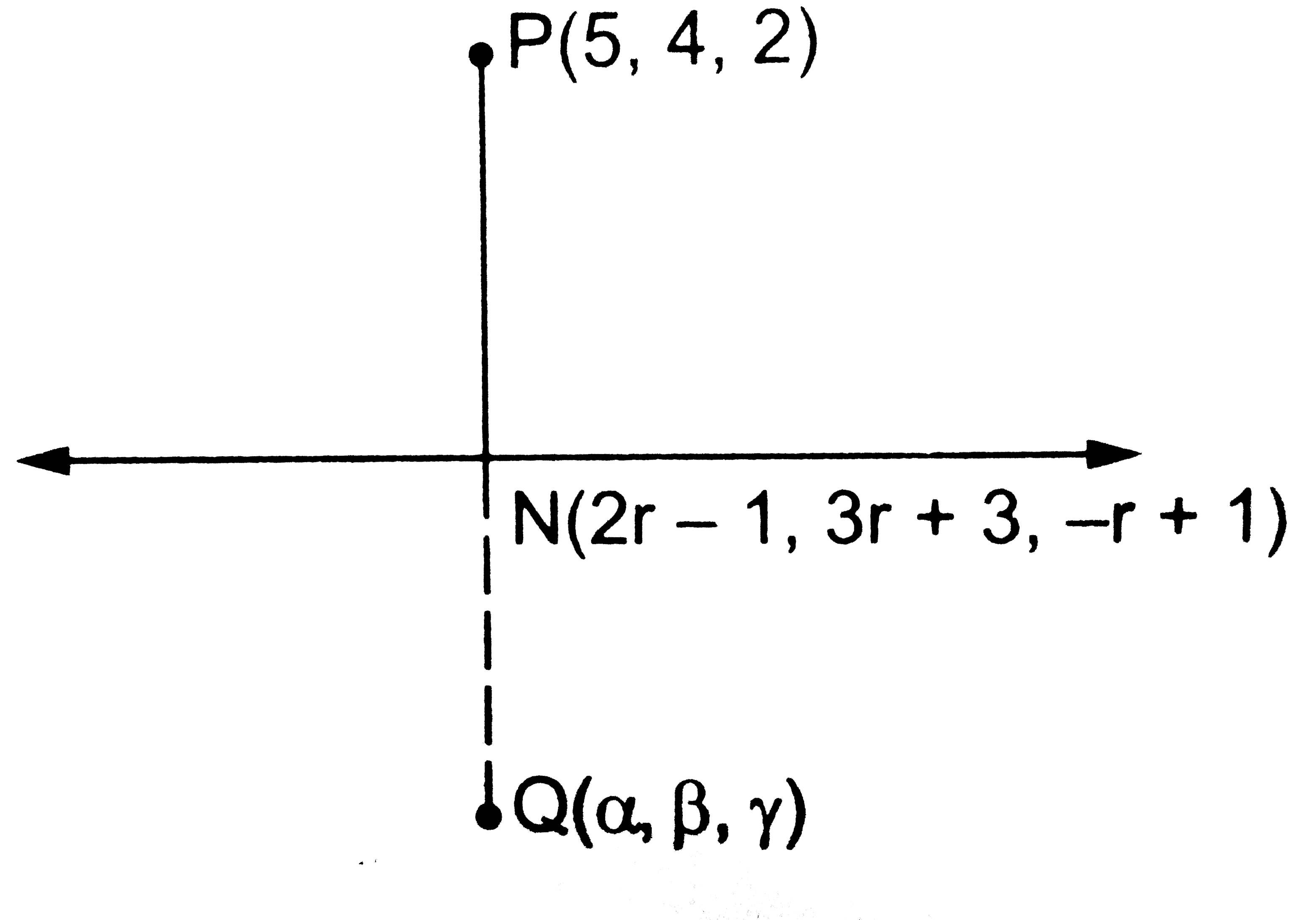
Clearly it passes through the point
(-1,3,1) and it has direction rations
2,3,-1
So, its Cartesian equations are
$\frac{x + 1}{2} = \frac{y - 3}{3} = \frac{z - 1}{- 1} = r$ (say)
The general point on this line is (2r -1, 3r+3,-r+1)
Let N be the foot of the perpendicular drawn from the point
$P (5, 4, 2)$ on the given line.
Then this point is $N (2 r - 6, 3 r + 3 - r + 1)$ for some fixed value of r.
D.r' s of PN are (2r-6 ,3r-1 ,-r -1)
D.r's of the given line are 2,3,-1
Since PN is perpendicular to the given line (i) we have
$2 (2 r - 6) + 3 (3 r - 1) - 1, (- r - 1) = 0 \Rightarrow 14 r = 14 \Rightarrow r = 1$
So , the point N is given byy N(1,6,0)
Hence the foot of the perpendicular from the given point P(5,4,2) on the given line is N(1,6,0)
Let $Q (α, β, γ)$ be the image of P(5,4,2) in the given line .
then N(1,6,0) is the midpoint of PQ.
$∴ \frac{5 + α}{2} = 1, \frac{4 + β}{2} 6 and \frac{2 + γ}{2} = 0 \Rightarrow α = - 3, β = 8 and γ = - 2$
Hence the image of P(5,4,2) in the given line is Q(-3,8-2)

Updated on:21/07/2023

The foot of the perpendicular from the point (1,2,3) on the line $\to r = (6 ˆ i + 7 ˆ j + 7 ˆ k) + λ (3 ˆ i + 2 ˆ j - 2 ˆ k)$ has the coordinates
A(5,8,15)
B(8,5,15)
C(3,5,9)
D(3,5,-9)
The position vector of the foot of the perpendicular draw from the point $2 ˆ i - ˆ j + 5 ˆ k$ to the line
$\to r = (11 ˆ i - 2 ˆ j - 8 ˆ k) + λ (10 ˆ i - 4 ˆ j - 11 ˆ k)$ is
A $ˆ i + 3 ˆ j + 2 ˆ k$
B $- ˆ i + 3 ˆ j - 2 ˆ k$
C $ˆ i - 3 ˆ j - 2 ˆ k$
D $ˆ i + 2 ˆ j + 3 ˆ k$