Question

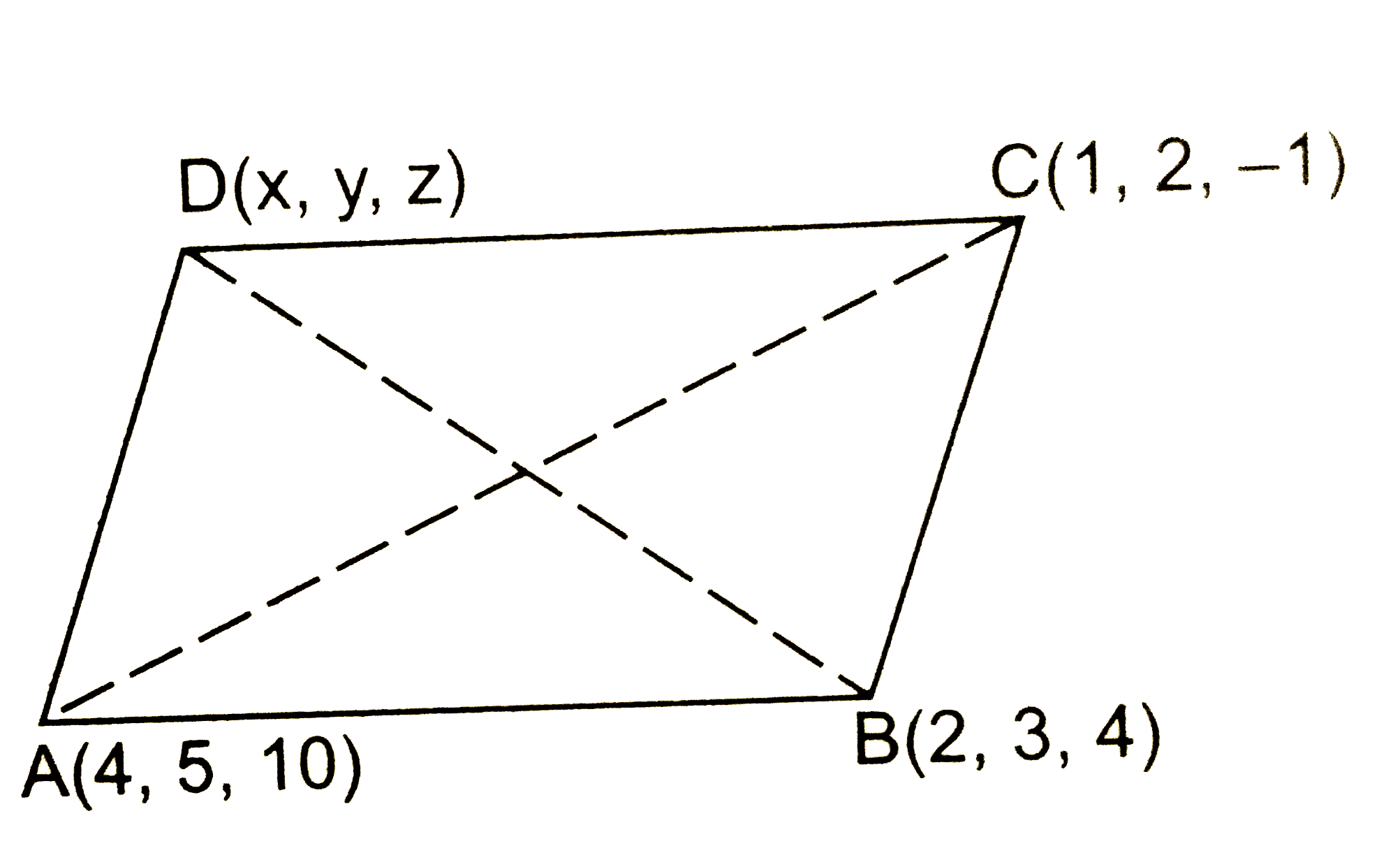
The
points A(4,
5, 10), B(2,
3, 4) and C (1,
2,-1) are three vertices of a parallelogram ABCD. Find the vector equations of
the sides AB and
BC and
also find the coordinates of point D.

Explanation

D.r's of side AB are (2-4) ,(3-5),(4-10) ,i.e., -2,-2 ,-6
Thus side AB passes through the point A(4,5,10) and it has D.r's -2,-2,-6

So, the vector equations of side AB is
`vec( r) =(4hat(i) +5hat(j) + 10hat(k)) +lambda (-2hat(i)-2hat(j) -6hat(K))`
D.r's of side BC are (1-2) ,(2-3) ,(-1-4),i.e., -1,-1,-5
Thus side BC passes through te point B(2,3,4) and it has d.r's
-1,-1,-5
So, the vector equations of side BC is
`vec(r )=(2hat(i) +3hat(j) +4hat(k)) +mu(-hat(i)- 3hat(j) -5hat(k))`
Let theh corrdinates of D be (x,y,z)
We know that midpoint of BD coincides with the midpoint of AC .
`:. (2+x)/(2)=(4+1)/(2),(3+y)/(2)=(5+2)/(2) " and " (4+z)/(2)=(10+(1-1))/(2)`
`rArr 2+x =5,3 +y =7 " and " 4+z =9`
`rArr x=3 ,y =4 " and " z=5`
`:.` coordinates of D are D(3,4,5)