In a group of 52 persons, 16 drinks tea but not coffee and 33 drink tea.
Find (i) how many drink tea and coffee both,
(ii) how many drink coffee but not tea.

Video Solution

Text Solution

Verified by Experts

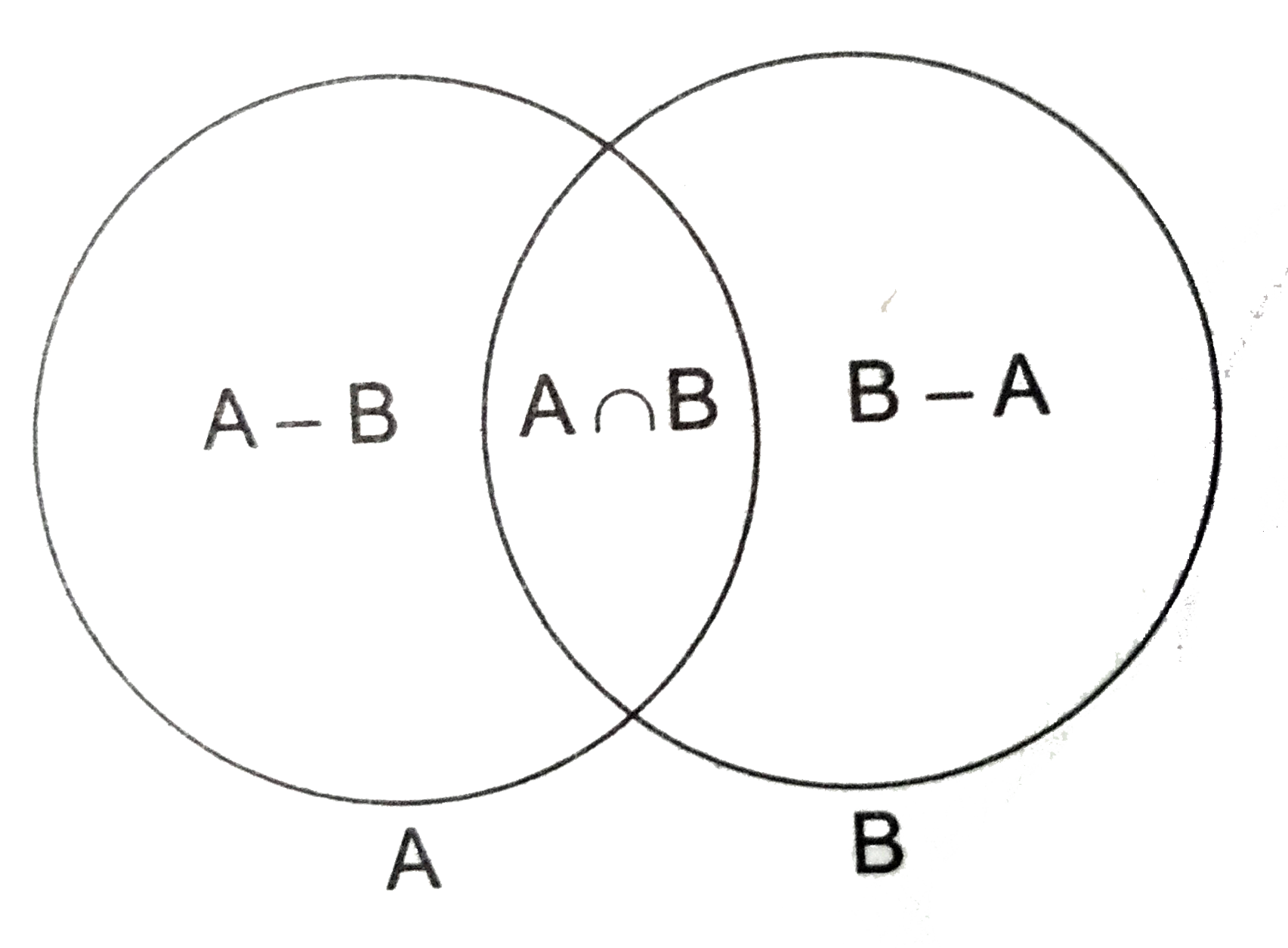
Let A = $s e t o f p r s o n s w h o d r \in k t e a and$ B= $s e t o f p e r s o n s w h o d r \in k c o f f e e . < b r > T h e n,$ (A-B)= $s e t o f p e r s o n s w h o d r \in k t e a b u t \neg c o f f e e . < b r > A n d,$ (B-A)= $S e t o f p e r s o n s w h o d r \in k c o f f e e b u t \neg t e a . < b r > G i v e n$ n(A cup B) $= 52, n (A - B) = 16 and n (A) = 33$ .
(i) Set of persons who drinks tea and coffee both $= (A \cap B)$ .
Now , $n (A - B) + n (A \cap B) = n (A)$
$\Rightarrow (A \cap B) = n (A) - n (A - B) = (33 - 16) = 17$ .
thus 17 persons drink tea and coffee both.
$(i i) n (A \cup B) = n (A) + n (B) - n (A \cap B)$
$\Rightarrow n (B) = n (A \cup B) + n (A \cap B) - n (A) = (52 + 17 - 33) = 36$ .
Now , $n (B - A) + n (A \cap B) = n (B)$ .
$\Rightarrow n (B - A) = n (B) - n (A \cap B) = (36 - 17) = 19$ .
Thus , numbers of persons who drink coffee but not tea 1=19.

Updated on:21/07/2023

In a group of 52 persons, 16 drink tea but not coffee and 33 drink tea. Then, the number of person who drink tea and coffee both
A18
B17
C16
D19
In a group of 52 persons, 16 drink tea but not coffee and 33 drink tea. Then, the number of person who drink tea and coffee both
A18
B17
C16
D19
In a group of 52 persons, 16 drink tea but not coffee and 33 drink tea. Then, the number of persons who drink coffee but not tea, is
A18
B19
C20
D21