A company has factories located at each of the two places P and Q. From these locations, a certain commondity is delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 7, 6 and 4 units of the commodity while the weekly production capacities of the factories at P and Q are respectively 9 and 8 units. The cost of transportation per unit is given below.
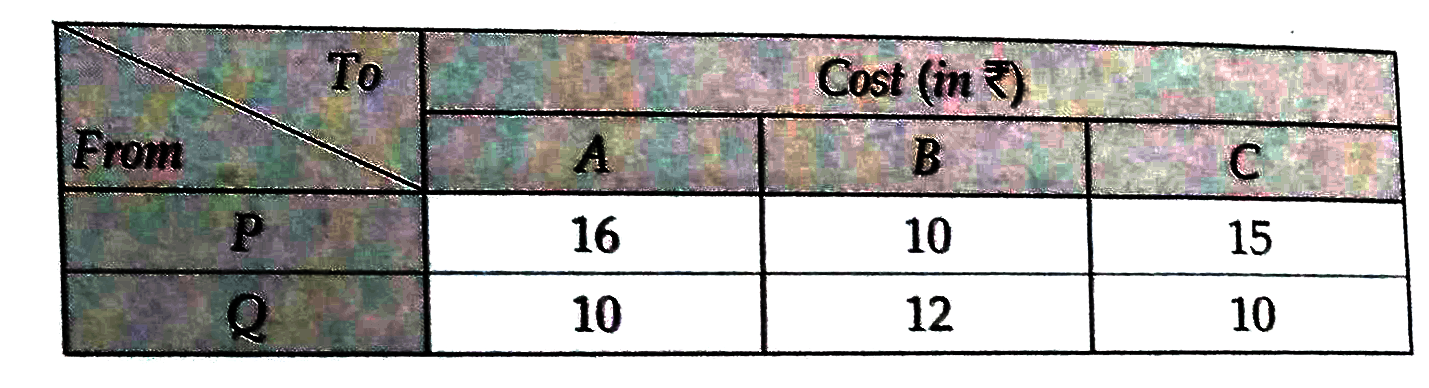
How many units should be transported from each factory to each depot in order that the tranporatin cost is minimum ? formulate the above LPP mathematically and then slove it.
This problem can be explained diagramatically as follows:
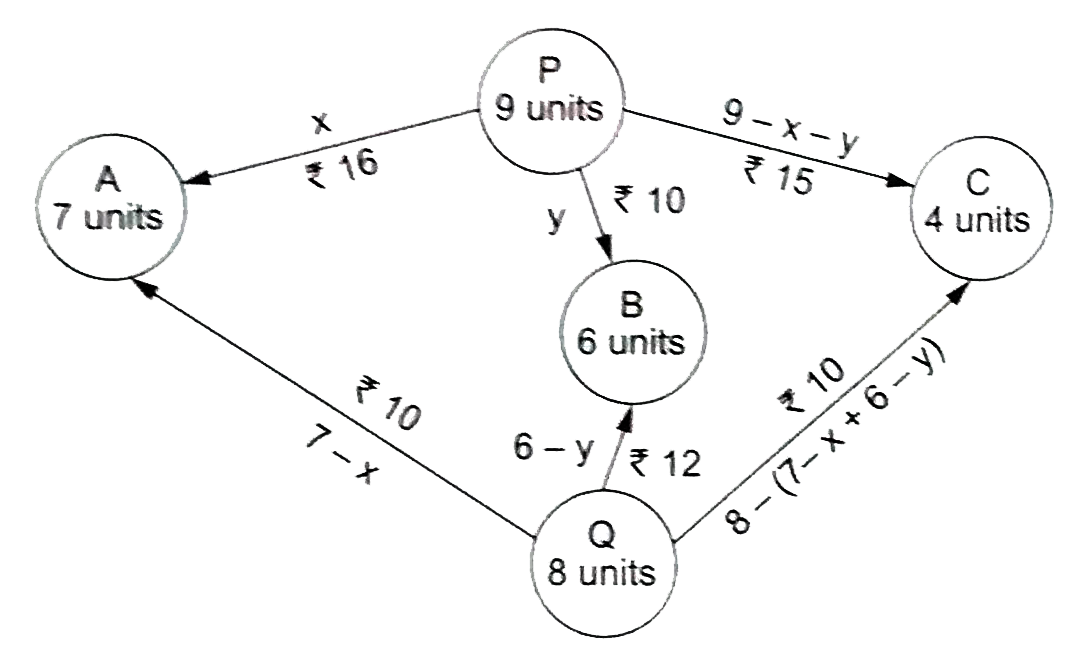
Let x units and y units of the commodity be transported from the factory at P to the depots at A and B respectively. Then, (9−x−y) units will be transported from the factor at P to the dpeot at C.
∴x≥0,y≥0,and9−x−y≥0⇒x+y≤9.
The weekly requirement of teh depot at A is 7 units. So, (7-x) units will be transported to A from the factor at Q.
Similarly, (6-y) units will be transported to B from the fctor at Q.
And, 8−(7−x+6−y)=(x+y−5) units will be transported to C from the factor at Q.
∴7−x≥0,6−y≥0andx+y−5≥0,
i.e.,x≤7,y≤6andx+y≥5.
The total cost of transportation is
Z=16x+10(7−x)+10y+12(6−y)+15(9−x−y)+10(x+y−5)
⇒Z=x−7y+227.
Now, we have to find the values of x and y which minimize
Z=x−7y+227, subject to the constraints
x≥0,y≥0,x+y≤7,y≤6andx+y≥5.
We draw th egraphs of the line
x=0,y=0,x+y=9,x=7,y=6andx+y=5
as shown below.

Since (0,0) satisfies x+y≤9, the line x+y=9 together with the region contining O(0,0) represents x+y≤9.
Since (0,0) does not satisfy x+y≥5, the line x+y=5 together with the region not containing O(0,.0) represents x+y≥5.
Since (0,0) satisfies x≤7, the line x=7 together with the region containing O(0,0) represents x≤7.
Since (0,0) satisfies y≤6, the line y=6 together with the region containing O(0,0) represents y≤6.
The y-axis and the region to its right-hand side represents x≥0.
The x-axis and the region above it represents y≥0.
Thus, teh shaded region represents the feasible region whose vertices are R, S, T, U, V and W.
On solving y=0andx+y=5, we get R(5,0).
On solving y=0andx=7, we get S(7,0).
On solving x=7andx+y=9, we get T(7,2).
On solving x+y=9andy=6, we get U(3,6).
On solving x=0andy=6, we get V(0,6).
On solving x=0andx+y=5, we get W(0,5).
The values of Z=x−7y+227atR,S,T,U,V and W we 232,234,220,188,185 and 192 respectively.
Thus, XZ is minimum at V(0,6). i.e., when x=0andy=6.
∴ from the factor at P there ust be a delivery of 0,6 and 3 units to A, B, C respectively.
And, the factory at Q must deliver 7,0 O and 1 units to A, B, C respectively.
Similar Questions
(Transportation problem) There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below :
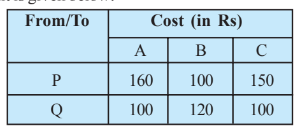
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
View SolutionThere are two factories located one at place P and the other at place Q.From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirments of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
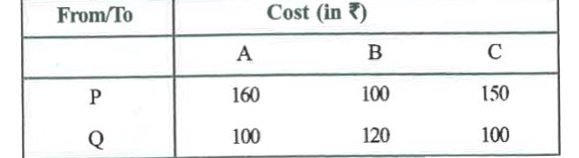
How many units should be transported from each factory to each depot in order that the transportable cost is minimum? When will be the minimum transportation cost?
View Solution
Knowledge Check

The products P & Q are respectivelyA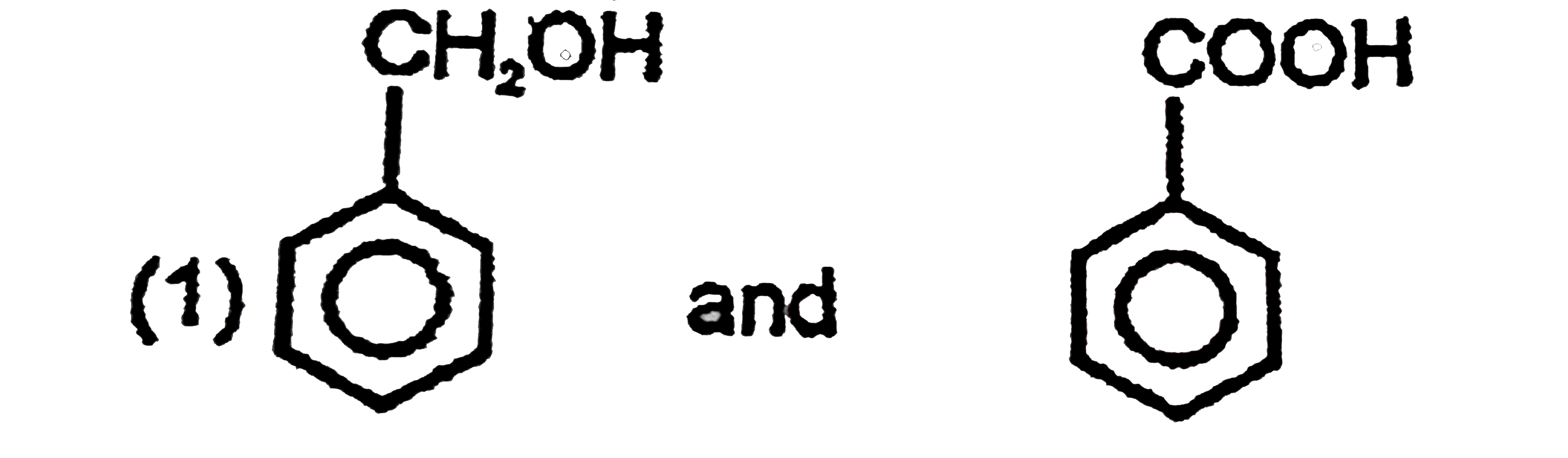 B
B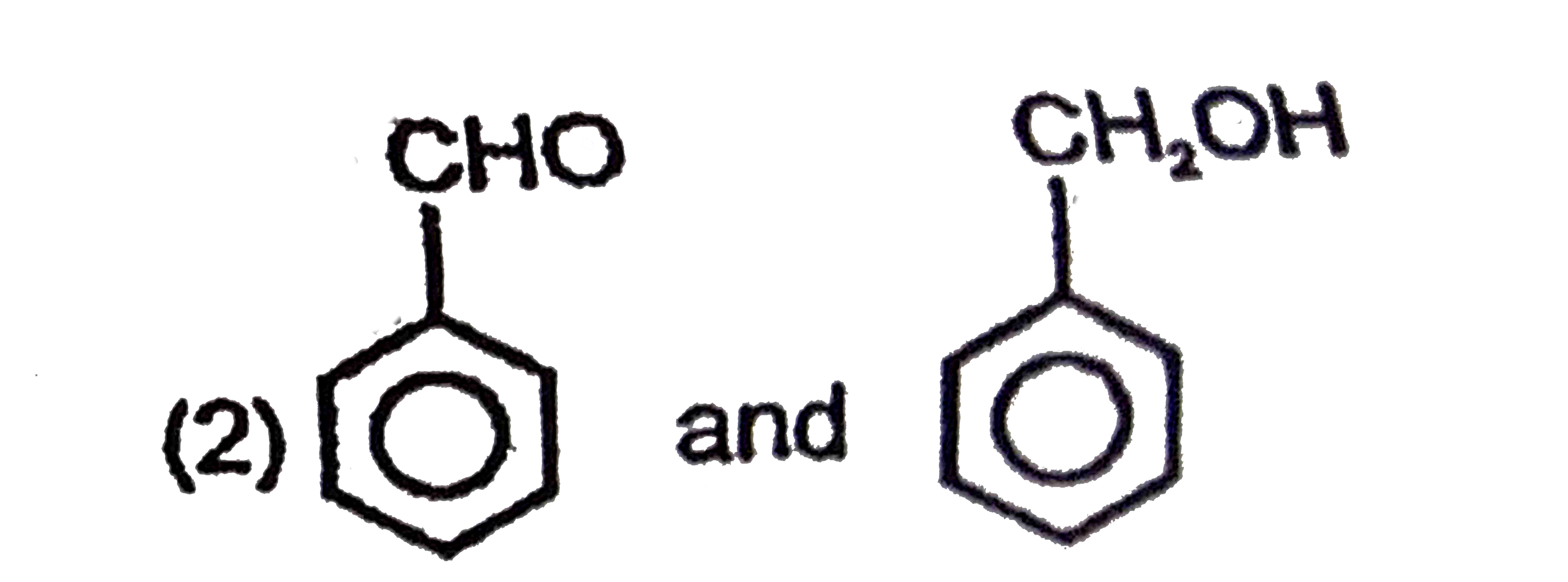 C
C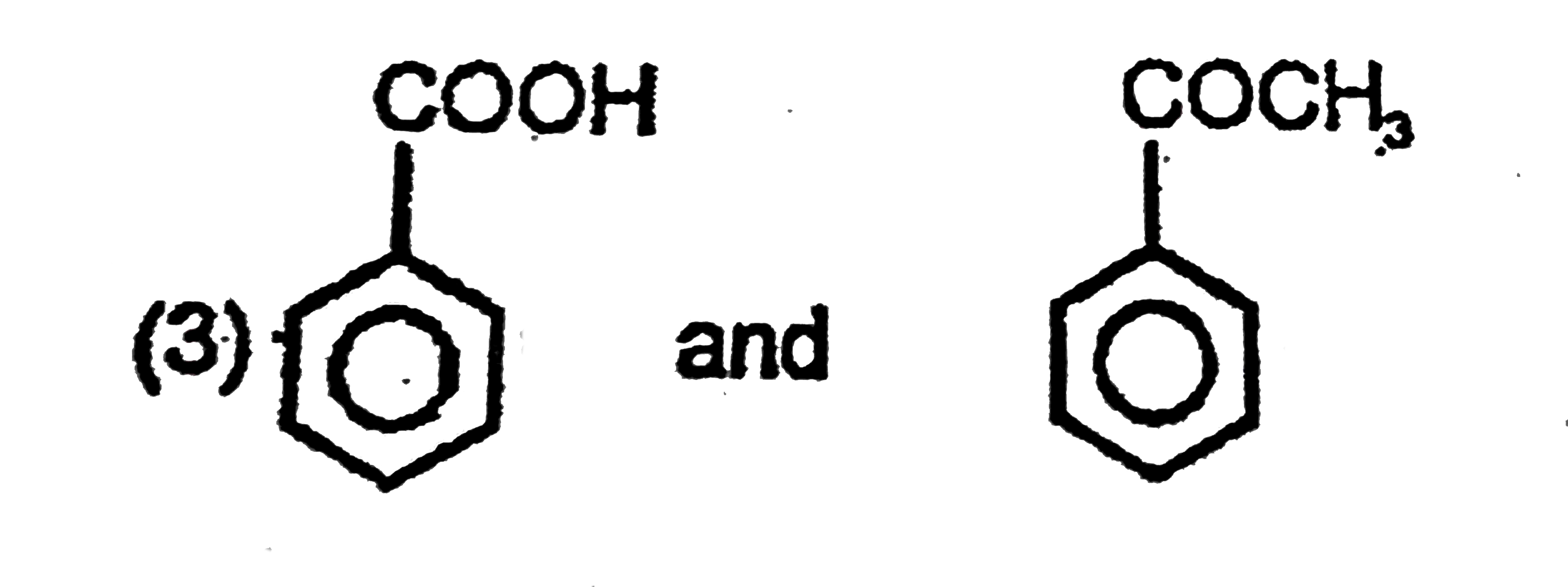 D
D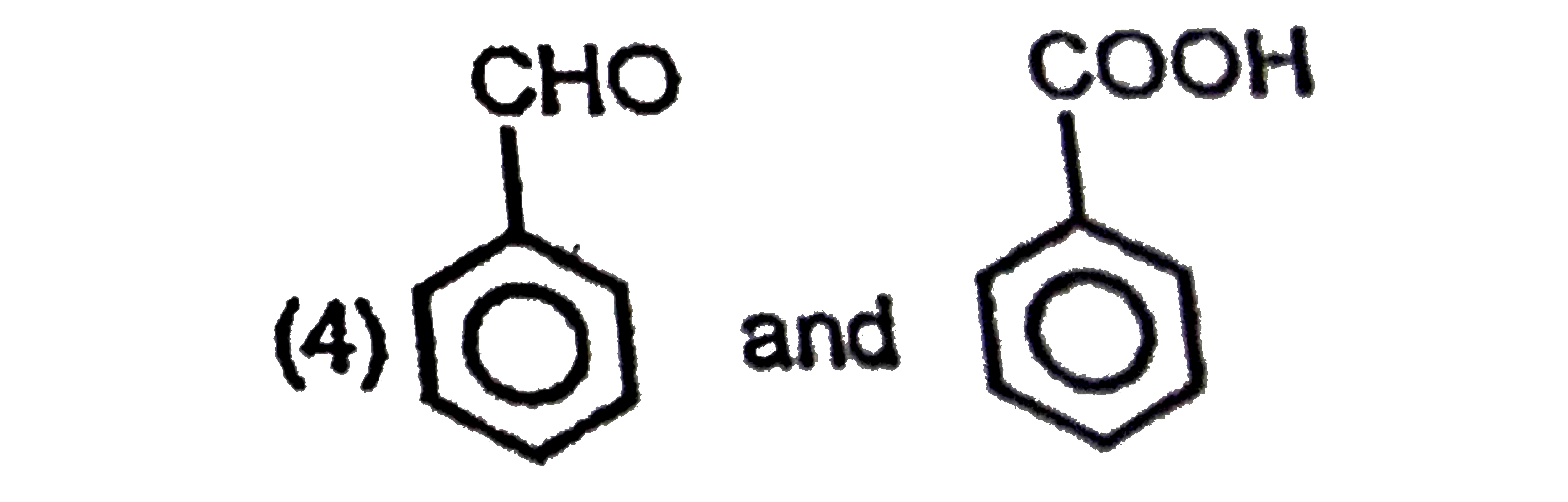
Two particles P and Q are located at distance rpandrQ respectively form the centre of rotating disc such that rP>rQ. The disc is rotating with constant angular acceleration. We can say
ABoth P and Q have the same acceelerationBBoth P and Q do not have any accelcrationCP has greater acceleration than QDQ has greater acceleration than PPhenol on treatment with dil. HNO3 gives two products P and Q. P is steam volatile but Q is not , P and Q are respectively-
A B
B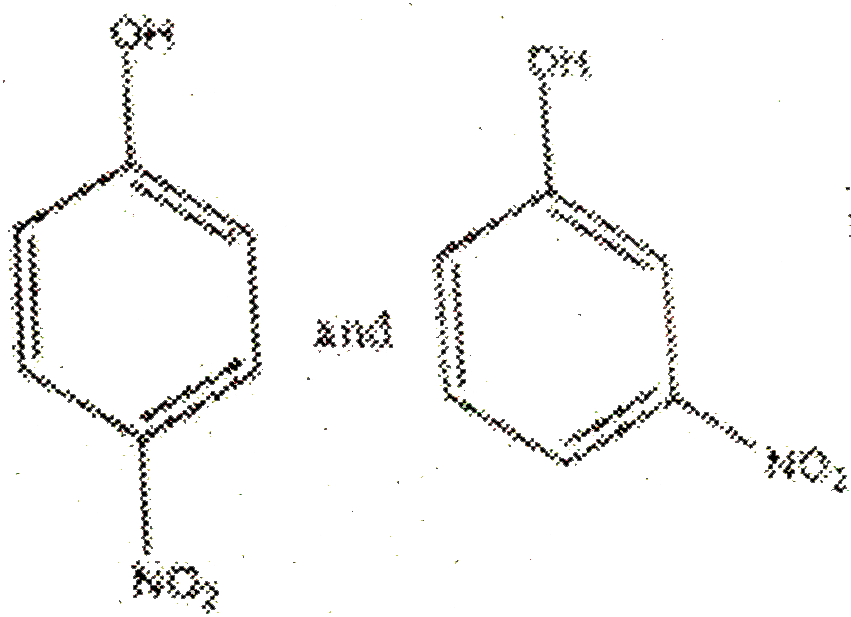 C
C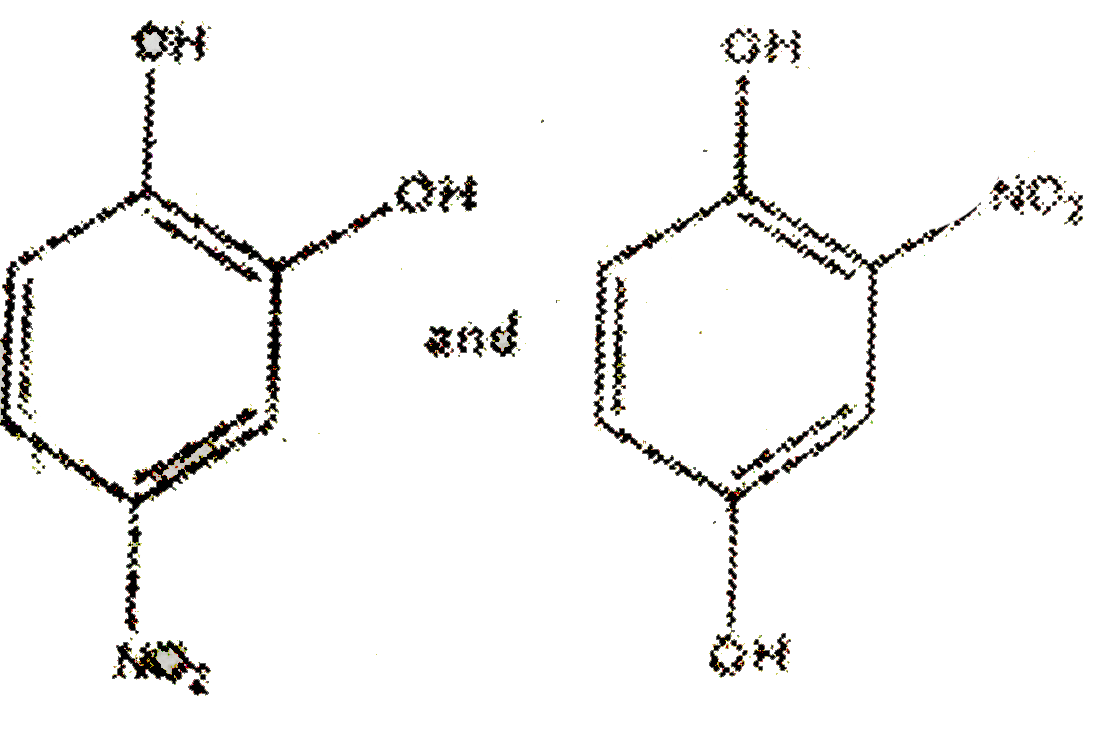 D
D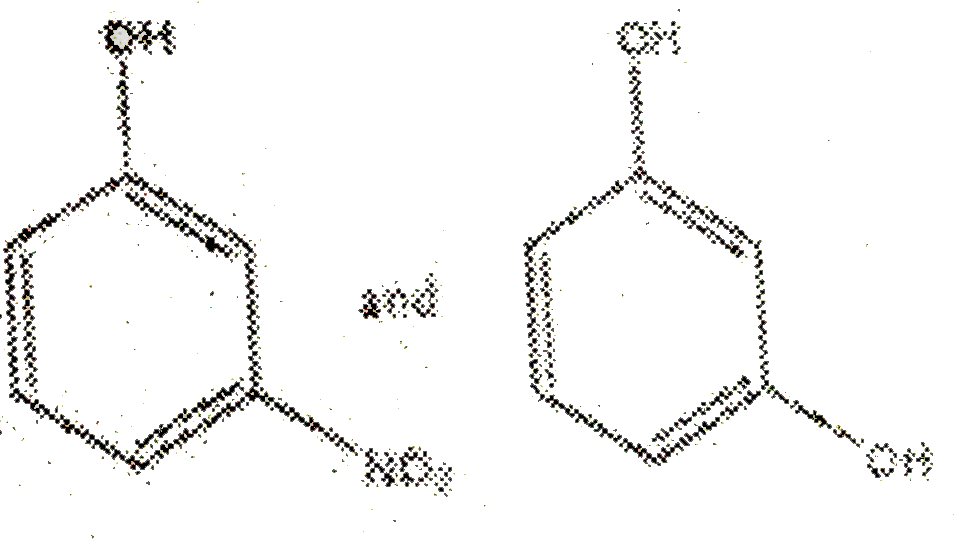
There are factories located one at place P and other at place Q from which a certin commodity is to be delivered to each of three depot situated at A,B and C. The weekly requirement of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below.
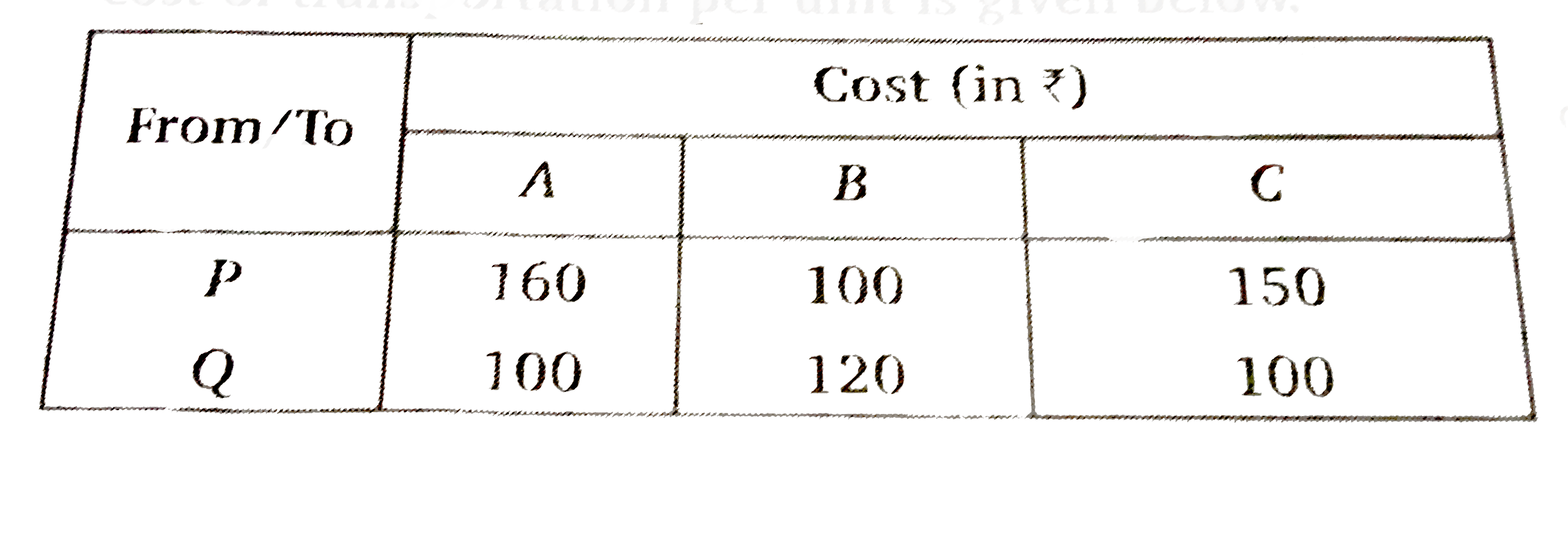
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. Also find the minimum transportation cost.
View Solution
Product (P) and (Q) respectively is :
View SolutionA medical company has factories at two places, A and B.From these places, supply is made to each of its three agencies situated at P,Q, and R.The monthly requirements of the agencies are respectively 40,40 and 50 packets of the medicines, while the production capacity of the factories A and B, are 60 and 60 packets respectively.The transportation cost per packet from the factories to the agencies are given below:

How many packets from each factory be transported to each agency so that the cost of transportation is minimum? Also find the minimum cost.
View SolutionFind the average cost of production ( in Rs per unit ) in factories in two states.

View SolutionAn oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:
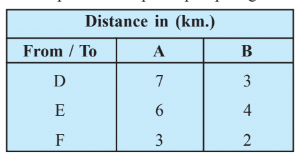
Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?
View Solution
