Let $n_{1} < n_{2} < n_{3} < n_{4} < n_{5}$ be positive integers such that $n_{1} + n_{2} + n_{3} + n_{4} + n_{5} = 20 .$ then the number of such distinct arrangements $n_{1}, n_{2}, n_{3}, n_{4}, n_{5}$ is

Video Solution

Text Solution

Verified by Experts

The correct Answer is:7

PLAN Reducing the equation to a newer equation, where sum of variables is less. Thus, finding the number of arrangements becomes easier.
As $n_{1} \geq 1, n_{2} \geq 2, n_{3} \geq 3, n_{4} \geq 4 n_{5} \geq 5$
Let $n_{1} - 1 = x_{1} \geq 0, n_{2} - 2 = x_{2} \geq 0, ..., n_{5} - 5 = x_{5} \geq 0$
$\Rightarrow$ New equation will be
$x_{1} + 1 + x_{2} + 2 + ... + x_{5} + 5 = 20$
$\Rightarrow x_{1} + x_{92}) + x_{3} + x_{4} + x_{5}) = 20 - 15 = 5$
Now, $x_{1} \leq x_{2} \leq x_{3} \leq x_{4} \leq x_{5}$

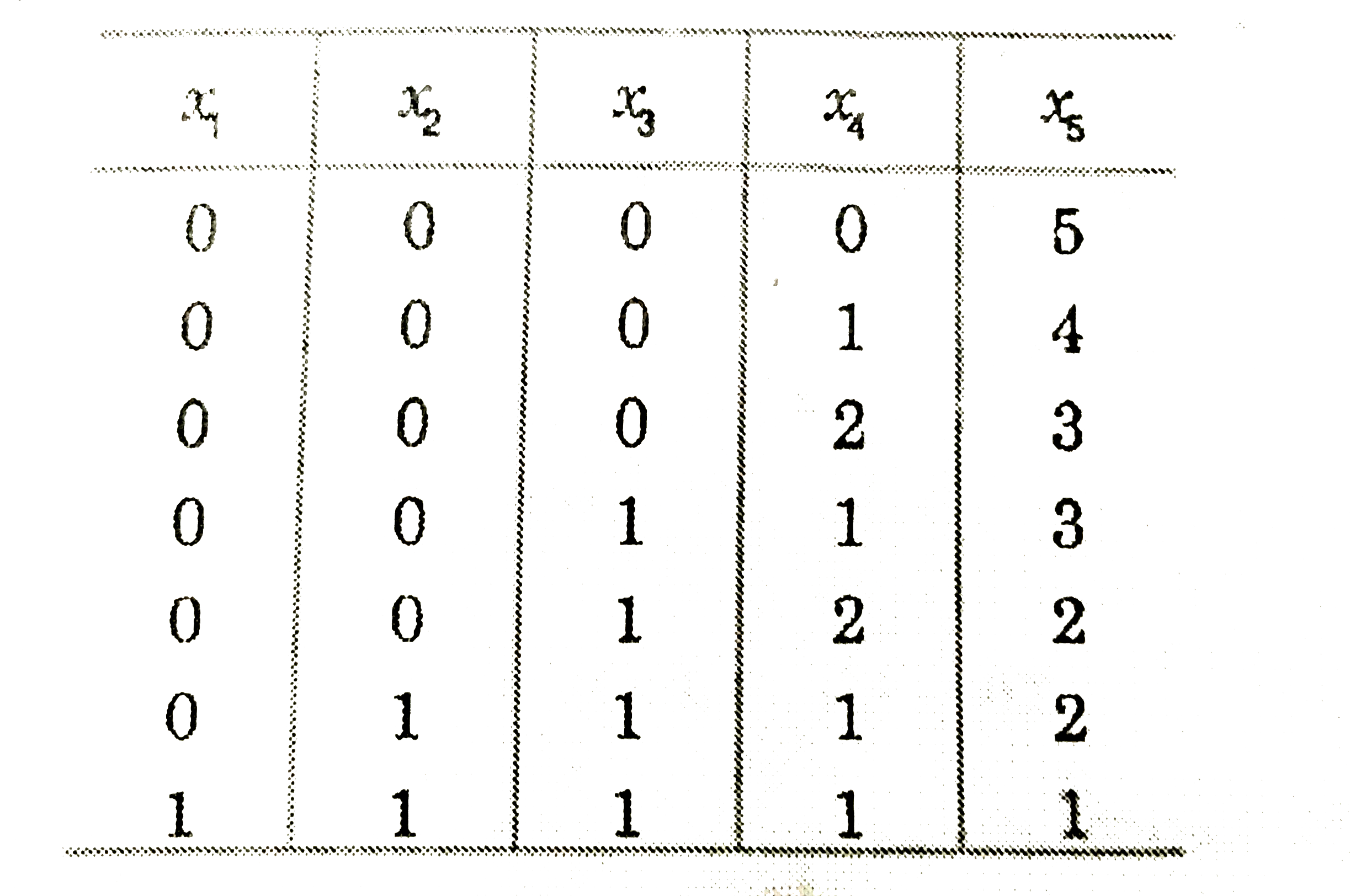
So, 7 possible cases will be there.

|

Updated on:21/07/2023

Class 12 MATHS PERMUTATIONS AND COMBINATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $n \geq 1, n \in Z$ . The real number $a \in 0, 1$ that minimizes the integral $\int_{0}^{1} | x^{n} - a^{n} | d x$ is
A $\frac{1}{2}$
B2
C1
D $\frac{1}{3}$
Question 2 - Select One
Let $a_{n} = {(1 + \frac{1}{n})}^{n} .$ Then for each $n \in N$
A $a_{n} \geq 2$
B $a_{n} < 3$
C $a_{n} < 4$
D $a_{n} < 2$
Question 3 - Select One
Let $P (n) : 1 + \frac{1}{4} + \frac{1}{9} + \dots . + \frac{1}{n^{2}} < 2 - \frac{1}{n}$ , is true
A $\forall n$
Bfor n=1
CFor $n > I, \forall n \in N$
DNone of these

IIT JEE PREVIOUS YEAR-PERMUTATIONS AND COMBINATIONS-Multinomial, Repeated Arrangement and Selection (Integer )

Home
Ask Doubt
Profile