Let √3ˆi+ˆj,ˆi+√3ˆj and βˆi+(1−β)ˆj respectively be the position vectors of the points A, B and C with respect to the origin O. If distance of C from the bisector of the acute angle between OA and OB is 3√2, then the sum of all possible values of β is (a) 1 (b) 3 (c) 4 (c) 2
1
3
4
2
The correct Answer is:A
According to given information, we have the following figure.
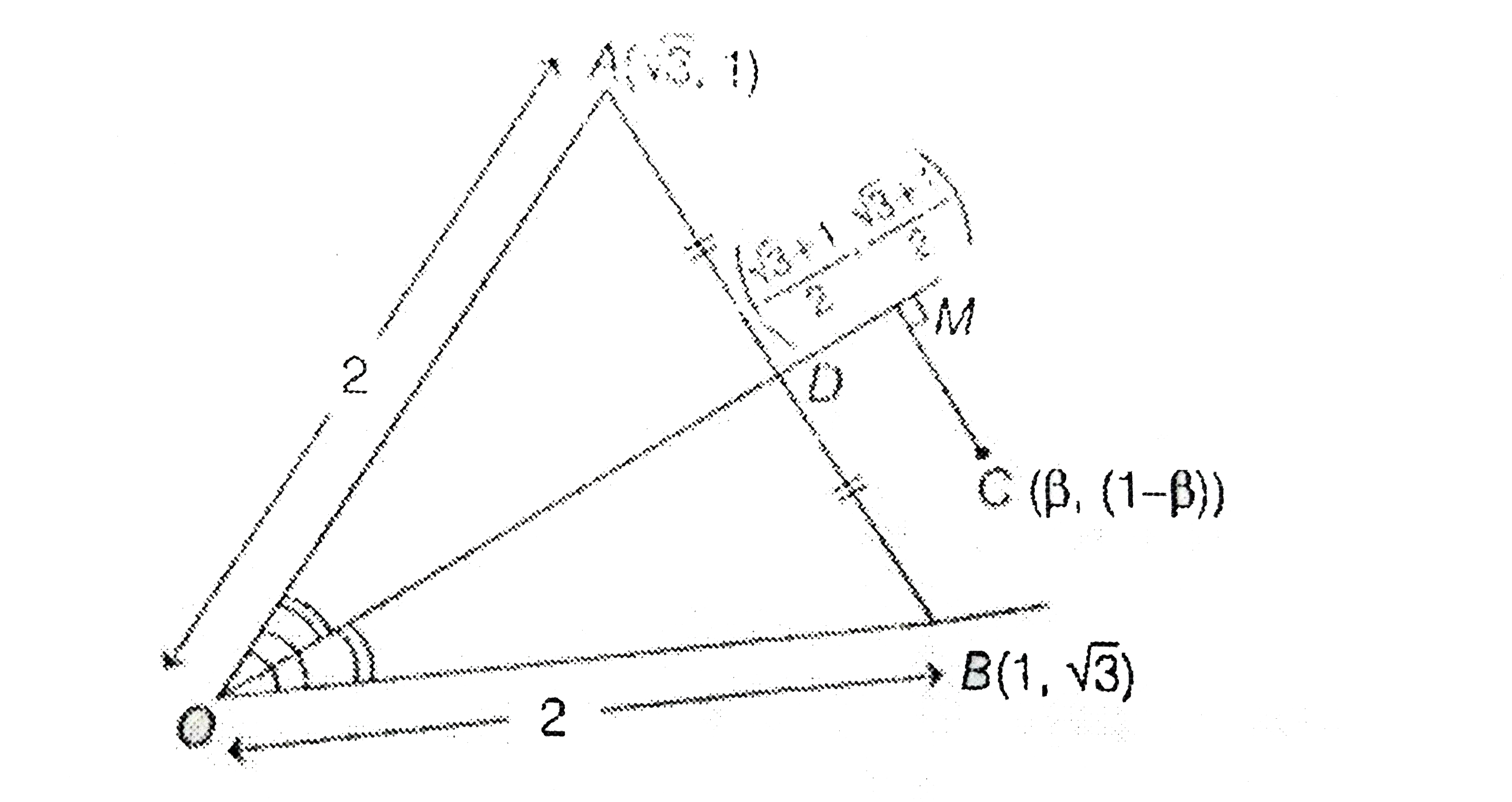
Clearly, angle bisector divides the sides AB in OA:OB,
i.e.,2:2=1:1 [using∠bisec→rtheorem]
So, D is the mid-point of AB and hence coordinates of D are (√3+12,√3+12)
Now, eauation of bisector OD is
(y−0)=⎛⎜⎝√3+12−0√3+12−0⎞⎟⎠(x−0)⇒y=x
⇒x−y=0
According to the problem,
3√2=CM=∣∣∣β−(1−β)√2∣∣∣
[Distance of a point P(x1,y1) from the line ax+by+c=0 is ∣∣∣ax1+by1+c√a2+b2∣∣∣]
⇒ |2β−1|=3⇒2β=±3+1
⇒ 2β=4,−2⇒β=2,−1
Sum of 2 and -1 is 1.
Topper's Solved these Questions
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Straight Line in Space and Shortest Distance Objective Question II (One or more than one correct option)
3 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question I (Only one correct option)
49 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)
1 Videos
- PROPERTIES OF TRIANGLESBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - CIRCUMCIRCLE, INCIRCLE, ESCRIBED CIRCLE, ORTHOCENTRE,INCENTRE AND CIRCUMCENTRE
20 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
8 Videos
Similar Questions
Let √3ˆi+ˆj,ˆi+√3ˆj and βˆi+(1−β)ˆj respectively be the position vedors of the points A, B and C with respect the origin O. If the distance of C from the bisector of the acute angle between OA and OB is 3√2, then the sum all possible values of β is _______.
View SolutionLet √3i+ˆj,ˆi+√3jandβˆi+(1−β)ˆj respectively be the position vedors of the points A, B and C with respect the origin O. If the distance of C from the bisector of the acute angle between OA and OB is 3√2, then the sum all possible values of β is _______.
View Solution
Knowledge Check
Let a=ˆi+ˆj+ˆk,b=ˆi−ˆj+ˆk and c=ˆi−ˆj−ˆk be three vectors.A vector v in the plane of a and b, whose projection on c is 1√3, is given
Aˆi−3ˆj+3ˆkB−3ˆi−3ˆj−ˆkC3ˆi−ˆj+3ˆkDˆi−3ˆj−3ˆkThe vector a=αˆi+2ˆj+βˆk lies in the plane of the vectors b=ˆi+ˆjandc=ˆj+ˆk and bisects the angle between b and c. Then, which one of the following gives possible value of αandβ?
Aα=1,β=1Bα=2,β=2Cα=1,β=2Dα=2,β=1The position vectors of the points A,B and C are ˆi+2ˆj−ˆk,ˆi+ˆj+ˆkand2ˆi+3ˆj+2ˆk, respectively. If A is chosen as the origin, then the position vectors of B and C are
Aˆi+2ˆk,ˆi+ˆj+3ˆkBˆj+2ˆk,ˆi+ˆj+3ˆkC−ˆj+2ˆk,ˆi−−ˆj+3ˆkD−ˆj+2ˆk,ˆi+ˆj+3ˆk
In R2 let √3i+ˆj,ˆi+√3jandβˆi+(1−β)ˆj respectively be the position vedors of the points X, Y and Z with respect the origin O. If the distance of Z from the bisector of the acute angle between OX and OY is 3√2, then the possible values of β is _______.
View SolutionPosition vector of ponts A,B,C are →a,→b,→c respectively which are by →a=√3ˆi+ˆj,→b=ˆi+√3ˆj,→c=βˆi+(1−β)ˆj. If distance of point C from angle bisector of OA and OB is 3√2 then value of β is (A) 1 (B) 2 (C) 4 (D) 3
View SolutionIf the position vectors of A and B are (√2−1)ˆi−ˆj and ˆi+(√2+1)ˆj respectively, then what is the magnitude of →AB?
View SolutionThe position vectors of the points A,B and C are ˆi+2ˆj−ˆk,ˆi+ˆj+ˆkand2ˆi+3ˆj+2ˆk, respectively. If A is chosen as the origin, then the position vectors of B and C are
View SolutionThe position vectors of the points A,B and C are (2ˆi+ˆj−ˆk),(3ˆi−2ˆj+ˆk) and (ˆi+4ˆj−3ˆk) respectively. Show that the points A,B and C are collinear.
View Solution
