A line with positive direction cosines passes through the point P(2, – 1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals

A

1

B

$\sqrt{2}$

C

$\sqrt{3}$

D

2

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Since, $l = m = n = \frac{1}{\sqrt{3}}$

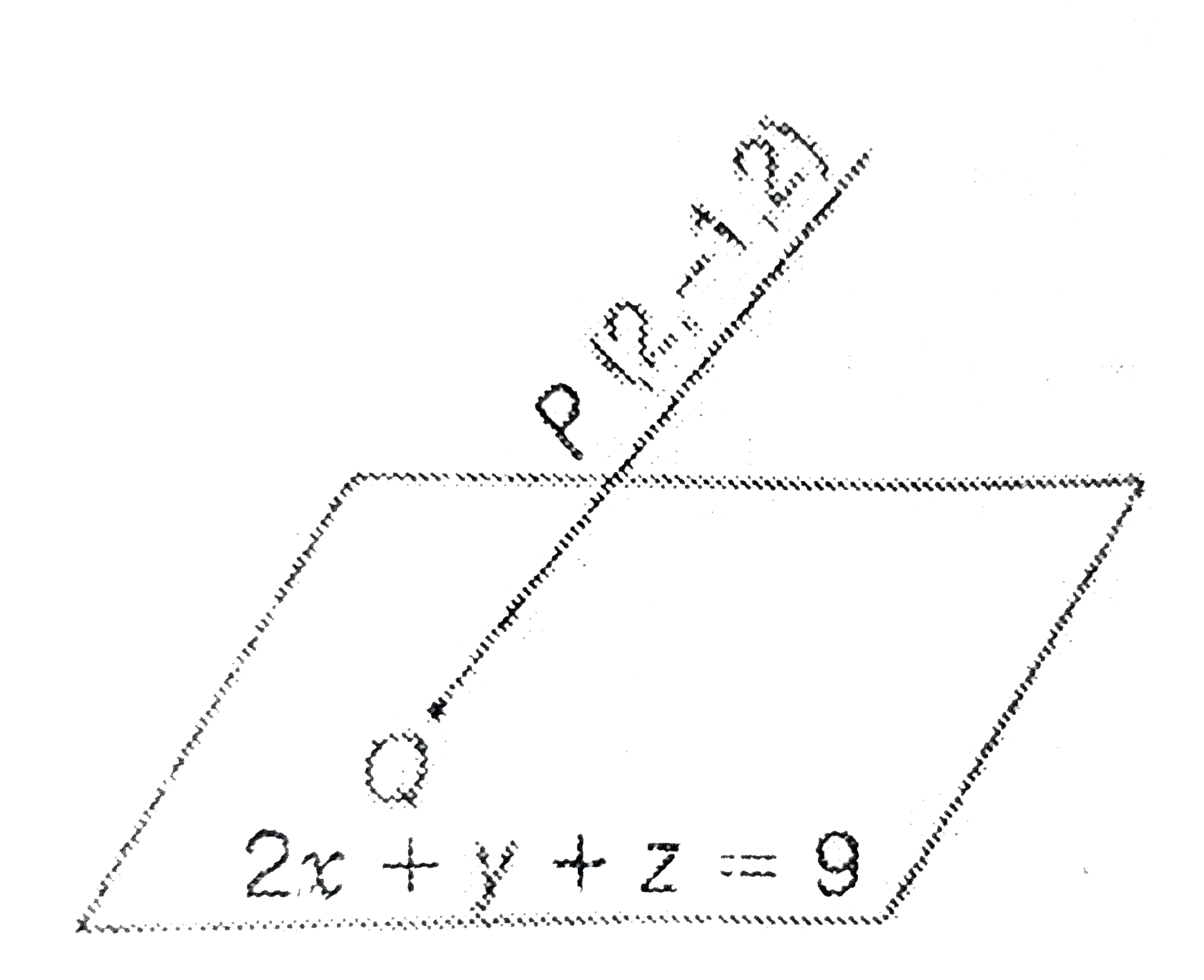
$∴ Equations of line are \frac{x - 2}{1 / \sqrt{3}} = \frac{y + 1}{1 / \sqrt{3}} = \frac{z - 2}{1 / \sqrt{3}}$
$\Rightarrow x - 2 = y + 1 = z - 2 = r [say]$
$∴$ Any point on the line is
$Q \equiv (r + 2, r - 1, r + 2)$
$∵$ Q lies on the plane $2 x + y + z = 9$
$∴ 2 (r + 2) + (r - 1) + (r + 2) = 9$
$\Rightarrow 4 r + 5 = 9 \Rightarrow r = 1$
$\Rightarrow Q (3, 0, 3)$
$∴ P Q = \sqrt{{(3 - 2)}^{2} + {(0 + 1)}^{2} + {(3 - 2)}^{2}} = \sqrt{3}$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A line with positive direction cosines passes through the point P(2, – 1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals
A1
B $\sqrt{2}$
C $\sqrt{3}$
D2
Question 2 - Select One
If a line passes through the point P(1, 2) makes an angle of $45^{\circ}$ with the x axis and meets the line x + 2y - 7 = 0 in Q, then PQ equals
AA) $\frac{2 \sqrt{2}}{3}$
BB) $\frac{3 \sqrt{2}}{2}$
CC) $\sqrt{3}$
DD) $\sqrt{2}$
Question 3 - Select One
A normal line with positive direction cosines to the plane P makes equal angles with the coordinate axis. The distance of the point A(1, 2, 3) from the line $\frac{x - 1}{1} = \frac{y + 2}{1} = \frac{z - 3}{2}$ measured parallel to the plane P is equal to
A3 units
B $\sqrt{13}$ units
C $\sqrt{14}$ units
D $2 \sqrt{5}$ units

IIT JEE PREVIOUS YEAR-3D Geometry-Equation of Plane Objective Question I (Only one correct option)

Home
Ask Doubt
Profile