The position of a particle moving along the x axis is given in centimeters by x=9.75+1.50t3, where t is in seconds. Calculate (a) the average velocity during the time interval t=2.00s to t=3.00s, (b) the instantaneous velocity at t=2.00s , (c) the instantaneous velocity at t=3.00s, (d) the instantaneous velocity at t=2.50s, and (e) the instantaneous velocity when the particle is midway between its positions at t=2.00s and t=3.00s . (f) Graph x versus t and indicate your answers graphically
KEY IDEA
We use Eq. 2-2 for average velocity and Eq. 2-4 for instantaneous velocity, and work with distances in centimeters and times in seconds.
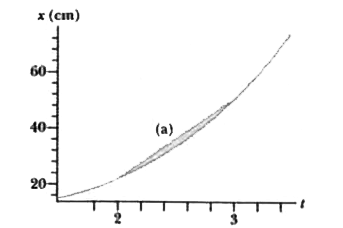
Calculations : (a) We plug into the given equation for x for t=2.00s and t=3.00s and obtain x2=21.75cm and x3=50.25cm, respectively. The average velocity during the time interval 2.00≤t≤3.00s is
vavg=ΔxΔt=50.25cm−21.75cm3.00s−2.00s
which yields vavg=28.5cm/s.
(b) The instantaneous velocity is v=dxdt=4.5t2, which, at time t=2.00s, yields v=(4.5)(2.00)2=18.0cm/s.
(c) At t=3.00s, the instantaneous velocity is
v=(4.5)(3.00)2=40.5cm/s.
(d) At t=2.50s, the instantaneous velocity is
v=(4.5)(2.50)2=28.1cm/s.
(e) Let tm stand for the moment when the particle is midway between x2 and x3 ( that is, when the particle is at xm=(x2+x3)/2=36cm). Therefore,
xm=9.75+1.5t3m⇒tm=2.596
in seconds. Thus, the instantaneous speed at this time is v=4.5(2.596)2=30.3cm/s.
(f) The answer to part (a) is given by the slope of the straight line between t=2 and t=3 in this x-vs-t plot. The answers to parts (b), (c), (d), and (e) correspond to the slopes of tangent lines ( not shown but easily imagined ) to the curve at the appropriate points.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - SAMPLE PROBLEM 2.042videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - SAMPLE PROBLEM 2.022videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
The position of the particle moving along x-axis is given by x=2t−3t2+t3 where x is in mt and t is in second.The velocity of the particle at t=2sec is
View SolutionThe displacement of a particle moving along an x axis is given by x=18t+5.0t2, where x is in meters and t is in seconds. Calculate (a) the instantaneous velocity at t=2.0s and (b) the average velocity between t=2.0s and t=3.0s.
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: x=2+9t+3t2−t3, where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionThe intantaneous coordinates of a particle are x=(8t−1)m and y=(4t2)m. Calculate (i) the average velocity of the particle during time interval from t=2s to t=4s (ii) the instantaneous velocity of the particle at t=2s.
View SolutionA particle is moving in a straight line. Its displacement at any instant t is given by x=10t+15t3, where x is in meters and t is in seconds. Find
(i) the average acceleration in the intervasl t = 0 to t = 2s and
(ii) instantaneous acceleration at t = 2 s.View SolutionThe position of a particle moving along the straight line is given as s= (t^(2)-4t+3)m where t is time in s .The magnitude of displacement of the particle during time interval t=0 to till its velocity becomes zero
View SolutionThe position of an object moving along x-axis is given by a+bt2, where a=8.5 m and b=2.5m/s2 and t is measured in seconds. The average velocity (in m/s) of the object between t=2s and t=4s is
View SolutionA particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
View SolutionThe position of a particle along the x-axis is given by the equation, x=t3−6t2+9t, where t is measured in seconds and x in meters.
(a) Find the velocity at time t
(b) What is the velocity at t = 2 s, at = t = 4 s?
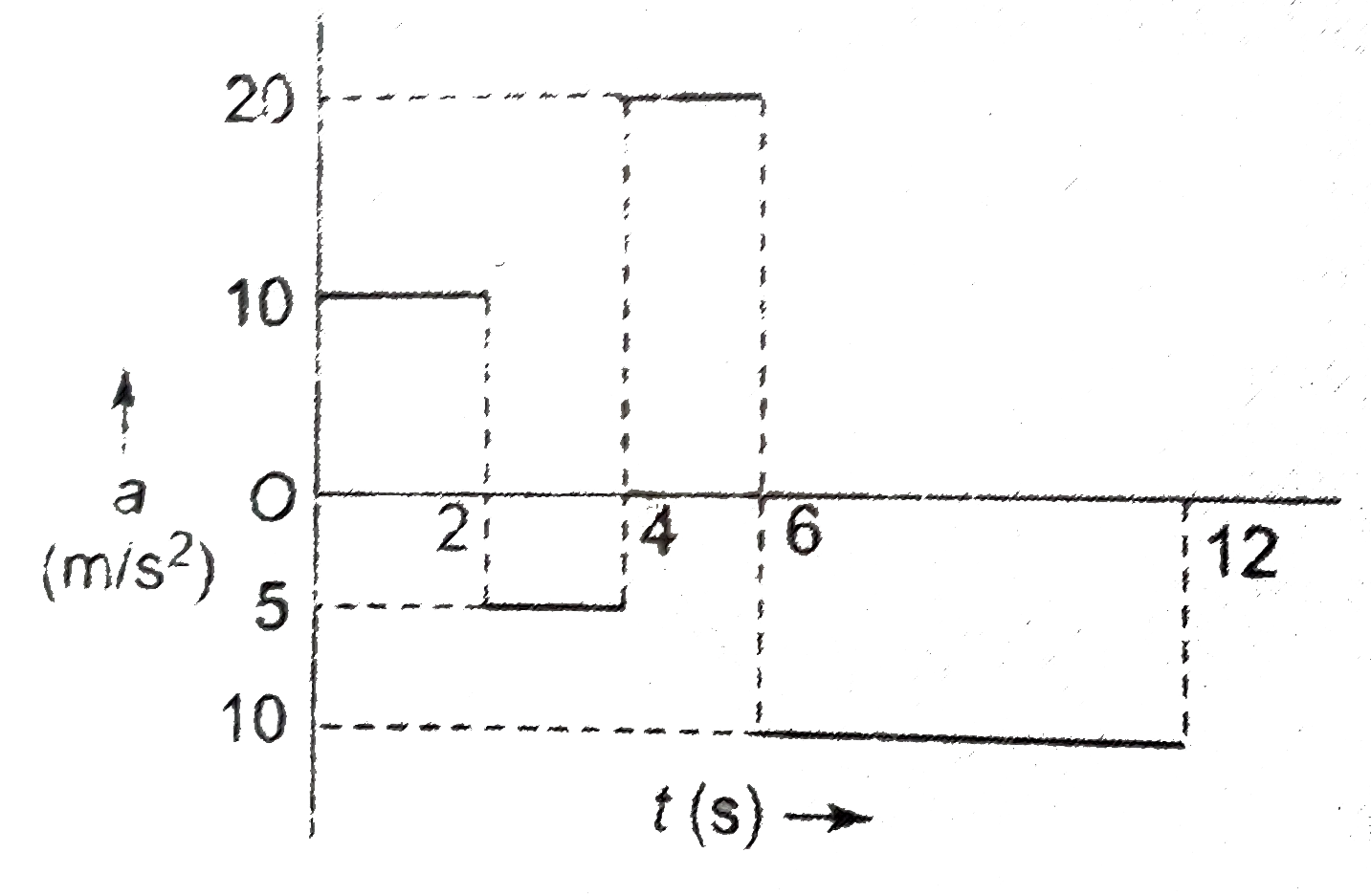
(c) What is the time instant, when particle is at rest?View SolutionA particle is moving along the x-axis. Consider it’s a-t graph. If initial velocity is 10 m//s, sketch the v-t graph and calculate the displacement in the time interval t=0 to 12 s.
 View Solution
View Solution

