A golf takes three putts to get the ball into the hole. The first putt displaces the ball 3.66 m north, the second 1.83 m southeast, and the thirs 0.91 m southwest. What are (a) the magnitude and (b) the direction of the displacement needed to get the ball into the hole on the first putt ?
To solve the problem step by step, we will break down the displacements into their vector components and then find the resultant vector that represents the displacement needed to get the ball into the hole in one putt.
Step 1: Represent the Displacements as Vectors
1. First Putt (A): The first putt displaces the ball 3.66 m north. In vector form, this can be represented as:
→A=3.66^j
2. Second Putt (B): The second putt displaces the ball 1.83 m southeast. Southeast is at a 45-degree angle between south and east. The components can be calculated as:
→B=1.83(cos(45∘)^i−sin(45∘)^j)
Since cos(45∘)=sin(45∘)=1√2:
→B=1.83(1√2^i−1√2^j)≈1.29^i−1.29^j
3. Third Putt (C): The third putt displaces the ball 0.91 m southwest. Southwest is also at a 45-degree angle but in the opposite direction. The components can be calculated as:
→C=0.91(−cos(45∘)^i−sin(45∘)^j)
Thus:
→C=0.91(−1√2^i−1√2^j)≈−0.64^i−0.64^j
Step 2: Calculate the Resultant Vector
Now, we can find the resultant vector →R by adding the three vectors:
→R=→A+→B+→C
Substituting the vectors:
→R=3.66^j+(1.29^i−1.29^j)+(−0.64^i−0.64^j)
Combining the components:
→R=(1.29−0.64)^i+(3.66−1.29−0.64)^j
Calculating the components:
→R=0.65^i+1.73^j
Step 3: Calculate the Magnitude of the Resultant Vector
The magnitude of the resultant vector →R can be calculated using the Pythagorean theorem:
|→R|=√(0.65)2+(1.73)2
Calculating:
|→R|=√0.4225+2.9929=√3.4154≈1.85 m
Step 4: Calculate the Direction of the Resultant Vector
The direction (angle θ) of the resultant vector can be found using the tangent function:
tan(θ)=RyRx=1.730.65
Calculating θ:
θ=tan−1(1.730.65)≈69.4∘
This angle is measured from the positive x-axis (east) towards the positive y-axis (north).
Final Answer:
(a) The magnitude of the displacement needed to get the ball into the hole in one putt is approximately 1.85 m.
(b) The direction of the displacement is approximately 69.4° north of east.
1. First Putt (A): The first putt displaces the ball 3.66 m north. In vector form, this can be represented as:
→A=3.66^j
→B=1.83(cos(45∘)^i−sin(45∘)^j)
Since cos(45∘)=sin(45∘)=1√2:
→B=1.83(1√2^i−1√2^j)≈1.29^i−1.29^j
→C=0.91(−cos(45∘)^i−sin(45∘)^j)
Thus:
→C=0.91(−1√2^i−1√2^j)≈−0.64^i−0.64^j
Now, we can find the resultant vector →R by adding the three vectors:
→R=→A+→B+→C
Substituting the vectors:
→R=3.66^j+(1.29^i−1.29^j)+(−0.64^i−0.64^j)
Combining the components:
→R=(1.29−0.64)^i+(3.66−1.29−0.64)^j
Calculating the components:
→R=0.65^i+1.73^j
The magnitude of the resultant vector →R can be calculated using the Pythagorean theorem:
|→R|=√(0.65)2+(1.73)2
Calculating:
|→R|=√0.4225+2.9929=√3.4154≈1.85 m
The direction (angle θ) of the resultant vector can be found using the tangent function:
tan(θ)=RyRx=1.730.65
Calculating θ:
θ=tan−1(1.730.65)≈69.4∘
This angle is measured from the positive x-axis (east) towards the positive y-axis (north).
(a) The magnitude of the displacement needed to get the ball into the hole in one putt is approximately 1.85 m.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS39videos
VECTORS
- BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - CHECKPOINT5videos
VECTORS
- BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)11videos
UNITS AND MEASUREMENT
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)5videos
WAVE - II
Similar Questions
A golfer takes his ball into the hole in the three strokes.The first stroke displaces the ball 4 m north , the second stroke 2 m south-east, and the third stroke 1 m south-west.What displacement would have been needed to get the ball into the hole in the first stroke ?
View SolutionA uniform ball, of mass M = 6.00 kg and radius R, rolls smoothly from rest down a ramp at angle θ=30.0∘ .
What are the magnitude and direction of the frictional force on the ball as it rolls down the ramp?View Solution
Knowledge Check
- Question 1 - Select One
A man first moves 3 m due east , them 6 m due north and finally 7 m due west , then the magnitude of the resultant displacement is (in metre)
A√16B√24C√52D√94 - Question 2 - Select One
A man first moves 3m due east, then 6m due north and finally 7m due west, then the magnitude of the resultant displacement is (in metre)
A√16B√24C√52D√94
At one instant a bicyclist is 30.0 m due east of a park's flagpole, going due south with a speed of 10.0 m/s. Then 30.0 s later, the cyclist is 40.0 m due north of the flagpole, going due east with a speed of 10.0 m/s. For the cyclist in this 30.0 s interval, what are the (a) magnitude and (b) direction of the displacement, the ( c) magnitude and (d) direction of the average velocity, and the (e) magnitude and (f) direction of the average acceleration?
View SolutionFigure shows a 0.300 kg baseball just before and just after it collides with a bat. Just before, the ball has velocity →v1 of magnitude 12.0 m/s and angle θ1=35.0∘ Just after, it is traveling directly upward with velocity →v2 of magnitude 10.0 m/s The duration of the collision is 2.00 ms. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the impulse on the ball from the bat? What are the (c) magnitude and (d) direction of the average force on the ball from the bat?
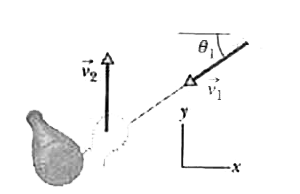 View Solution
View SolutionA golfer hits a golf ball into the air over level ground. The velocity of the ball at a height of 10.3 m is →v=(8.6ˆi+7.2ˆj)m/s, with ˆi horizontal and ˆj upward. Find (a) the maximum height of the ball and (b) the total horizontal distance traveled by the ball. What are the ( c) magnitude and (d) angle (below the horizonatl) of the balls velocity just before it touches the ground?
View SolutionThree small balls of equal mass (m) are suspended from a thread and two springs of same force constant (K) such that the distances between the first and the second ball and the second third ball are the same. Thus the centre of mass of the whole system coincides with the second ball. The thread supporting the upper ball is cut and system starts a free fall. Find the distance of the centre of mass of the system from the second ball when both the springs acquire their natural length in the falling system.
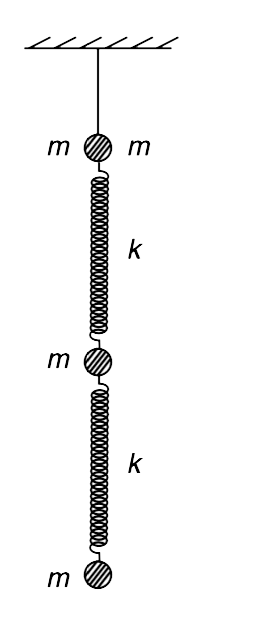 View Solution
View SolutionA ball of mass m strikes a rigid wall with speed v and gets reflected without any loss of speed, as shown in the figure.
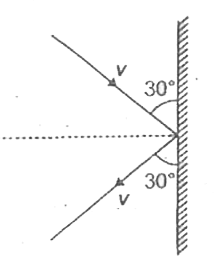
(a) What is the magnitude of the impulse imparted to the ball by the wall?
(b) What is the direction of the force on the wall due to the ball?View Solution6 balls marked as 1,2,3,4,5 and 6 are kept in a box. Two players A and B start to take out 1 ball at a time from the box one after another without replacing the ball till the game is over. The number marked on the ball is added each time to the previous sum to get the sum of numbers marked on the balls taken out. If this sum is even, then 1 point is given to the players. the first player to get 2 points is declared winner. at the start of the game, the sum is 0. if A starts to take out the ball, find the number of ways in which the game can be won.
View Solution

