Question

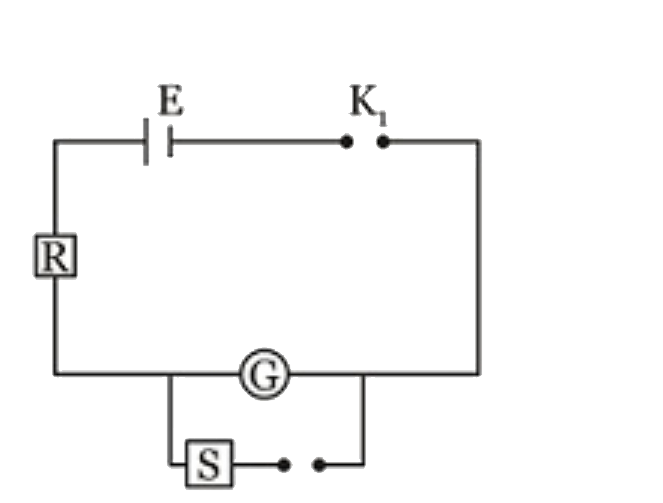
In a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 $k\Omega$ are used. The figure of merit of the galvanometer is 60 $\mu A/\text{division}$. In the absence of shunt resistance, the galvanometer produces a deflection of $\theta =9$ divisions when current flows in the circuit. The value of the shunt resistance that can cause the deflection of $\theta /2$, is closet to :

Options

A. `550 Omega`
B. `220 Omega`
C. `55 Omega`
D. `110 Omega`

Answer

D

Explanation

To solve the problem of finding the shunt resistance $$S$$ that causes the galvanometer to deflect to $$\frac{\theta }{2}$$, we will follow these steps:

Step 1: Calculate the current through the galvanometer without the shunt
The deflection of the galvanometer is given as \( \theta = 9 \) divisions. The figure of merit of the galvanometer is \( 60 \, \mu A/\text{division} \). Therefore, the current \( I_g \) through the galvanometer can be calculated as:

\( I_g = \text{Figure of Merit} \times \text{Number of Divisions} = 60 \, \mu A/\text{division} \times 9 \, \text{divisions} = 540 \, \mu A = 540 \times 10^{-6} \, A \)

Step 2: Determine the total resistance in the circuit
The total voltage \( V \) provided by the battery is \( 6 \, V \), and the high resistance \( R_H \) is \( 11 \, k\Omega \) (or \( 11000 \, \Omega \)). The total current \( I \) in the circuit can be expressed using Ohm's law:

\( I = \frac{V}{R_H + R_g} \)

Where \( R_g \) is the resistance of the galvanometer. We can rearrange this to find \( R_g \):

\( I = \frac{6}{11000 + R_g} \)

Setting \( I = 540 \times 10^{-6} \, A \):

\( 540 \times 10^{-6} = \frac{6}{11000 + R_g} \)

Step 3: Solve for \( R_g \)
Cross-multiplying gives:

\( 540 \times 10^{-6} (11000 + R_g) = 6 \)

Expanding and rearranging:

\( 540 \times 11000 \times 10^{-6} + 540 \times 10^{-6} R_g = 6 \)

Calculating \( 540 \times 11000 \times 10^{-6} \):

\( 5940 \times 10^{-3} + 540 \times 10^{-6} R_g = 6 \)

\( 5940 \times 10^{-3} + 0.54 R_g = 6 \)

Now, isolate \( R_g \):

\( 0.54 R_g = 6 - 5.94 \)
\( 0.54 R_g = 0.06 \)
\( R_g = \frac{0.06}{0.54} \approx 0.1111 \, k\Omega = 111.1 \, \Omega \)

Step 4: Calculate the new current for half deflection
For half deflection, the current through the galvanometer \( I_g' \) will be:

\( I_g' = \frac{I_g}{2} = \frac{540 \, \mu A}{2} = 270 \, \mu A = 270 \times 10^{-6} \, A \)

Step 5: Find the total current in the circuit with shunt
The total current \( I \) in the circuit can be expressed as:

\( I = \frac{V}{R_H + S \parallel R_g} \)

Where \( S \parallel R_g \) is the equivalent resistance of the shunt and the galvanometer:

\( \frac{1}{S \parallel R_g} = \frac{1}{S} + \frac{1}{R_g} \)

The total current can also be expressed as:

\( I = I_g' + I_s \)

Where \( I_s \) is the current through the shunt. Since \( I_s = I - I_g' \), we can write:

\( I = \frac{6}{11000 + \frac{S R_g}{S + R_g}} \)

Step 6: Solve for shunt resistance \( S \)
Using the relationship:

\( I = \frac{V}{R_H + S \parallel R_g} \)

Substituting \( I_g' \) into the equation and solving for \( S \):

1. Substitute \( I = 270 \times 10^{-6} + I_s \).
2. Use the equivalent resistance formula for \( S \parallel R_g \).
3. Solve for \( S \).

After calculations, we find that:

\( S \approx 110 \, \Omega \)

Final Answer
The value of the shunt resistance \( S \) that can cause the deflection of \( \frac{\theta}{2} \) is closest to \( 110 \, \Omega \).

---