The formula connecting u,v and f for a spherical mirror is valid only for mirrors whose sizes are very small compared to their radii of curvature. Because
Statement-2
Laws of reflection are strictly valid for plane surfaces, but nor for large spherical surfaces.s
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement -1.
Statement-1 is true, statement-2 is true, Statement-2 is Not a correct explanation for Statement -3
Statement-1 is true, statement-2 is false
Statement-1 is false, statement-2 is true
The correct Answer is:C
Step by step video, text & image solution for The formula connecting u,v and f for a spherical mirror is valid only for mirrors whose sizes are very small compared to their radii of curvature. Because Statement-2 Laws of reflection are strictly valid for plane surfaces, but nor for large spherical surfaces.s by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - MULTIPLE CHOICE QUESTIONS22videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - SECTION-III (Comprehension Type )3videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 36videos
JEE (ADVANCE) 2020
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-36videos
JEE ADVANCED 2020
Similar Questions
STATEMENT-1 The formula connecting u,v and f for a spherical mirrors whose sizes are very small compared to their radii of curvature.
STATEMENT-2 Laws of reflection are strictly valid for plane surfaces, but not for large spherical surfaces.View SolutionAssertion:- The formula (14+1u=1f) connecting u and v for a spherical mirror is valid only for mirros whose sizes are very small compared to their radii of curvatures.
Reason:- Laws of reflection are strictly valid for smaller size of of optical system.View Solution
Knowledge Check
- Question 1 - Select One
Statement - 1 : The formula connecting u, v and f for a spherical mirror is valid only for mirrors whose sizes are very small compared to their radii of curvature. Because
Statement - 2 : Laws of reflection are strictly valid for plane surfaces, but not for large spherical surfaces.AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for statement-1.BStatement-1 is True, Statement-2 is Tru, Statement-2 is not a correct explanantion for statement-1.CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is True. - Question 2 - Select One
In each of the questions, assertion(A) is given by corresponding statement of reason (R) of the statemens. Mark the correct answer.
Q. Statement I: The formula connecting u,v and f for a spherical mirror is valid only for mirrors whose sizes are very small compared to their radii of curvature.
Statement II: Laws of reflection are strictly valid for plane surfaces, but not for large spherical surfaces.AIf both Statement I and Statement II are true and Statement II is the correct explanation of Statement I.BIf both Statement I and Statement II are true but Statement II is not the correct explanation of Statement I.CIf Statement I is true, but Statement II is false.DIf Statement I is false, but Statement II is true. - Question 3 - Select One
Assertion The formula connecting u, v and f for a spherical mirror is valid only for mirrors sizes which are very small compared to their radii of curvature.
Reason Laws of reflection are stricity valid for plane surface, but not for large spherical.AIf both Assertion and Reason are true and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are true but Reason is not correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.
STATEMENT-1 Spherical aberration is a defeat of a spherical mirror,in which not all rays focus at single point.
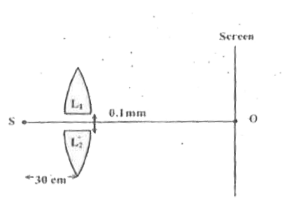
STATEMENT2 The laws of reflecion are not valid for all raysView SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
QDistance between the images Si and S2 will be
 View Solution
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Distance of a point from O, at which the sixth order minimum is formed, will be
 View Solution
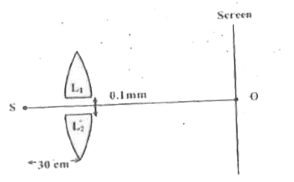
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Phase difference between the light waves 0.1 mm from along the screen, where intensity is half the maximum value, is
 View Solution
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q0.25 mm
 View Solution
View Solution

