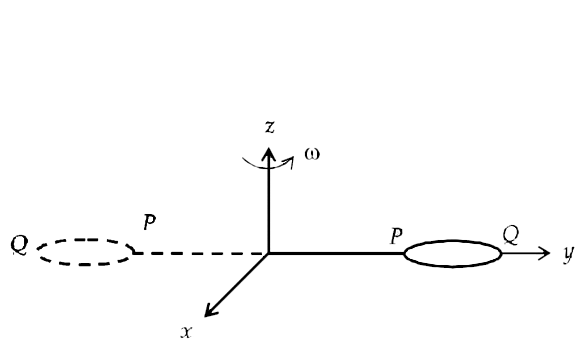
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case

Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis. 
It is vertical for both the cases (a) and (b).
It is vertical for case (a), and is at 45∘ to the x-z plane and lies in the plane of the disc for case (b).
It is horizontal for case (a), and is at 45∘ to the x-z plane and is normal to the plane of the disce for case (b).
It is vertical for case (a), and is at 45∘ to the x-z plane and is normal to the plane of the disc for case (b).
The correct Answer is:A
Step by step video & image solution for The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed omega the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed omega in this case Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45^@ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed omega about the z-axis. Which of the following statements about the instantaneous axis (passing through the centre of mass) is correct? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Section III : Multiple Correct Answer(s) Type
6 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PART I : PHYSICS (SECTION -1)
10 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Section I : Single Correct Answer Type
7 Videos
- JEE (ADVANCE) 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 3
6 Videos
- JEE ADVANCED 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-3
6 Videos
Similar Questions
In the given circuit, the AC source has (ω)=100rad/s. Considering the inductor and capacitor to be ideal, the correct choice(s) is (are)
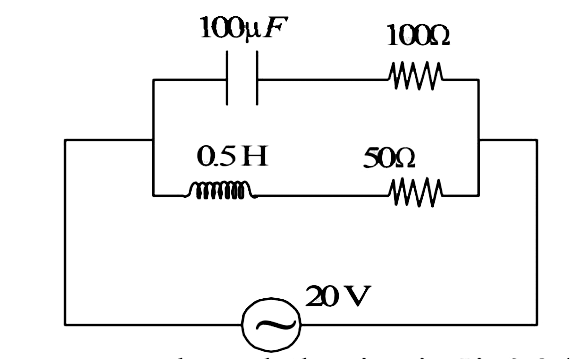 .
.
View SolutionThe diameter of a cylinder is measured using a vernier callipers with no zero error . It is found that the zero of the vernier scale lies between 5.10and5.15cm of the main scale . The 24th division of the vernier scale exactly coincides with one of the main scale divisions . The diameter of the cylinder is
View SolutionA loop carrying current I lies in the x−y plane as shown in the figure . The unit vector ˆk is coming out of the plane of the paper . The magnetic moment of the current loop is
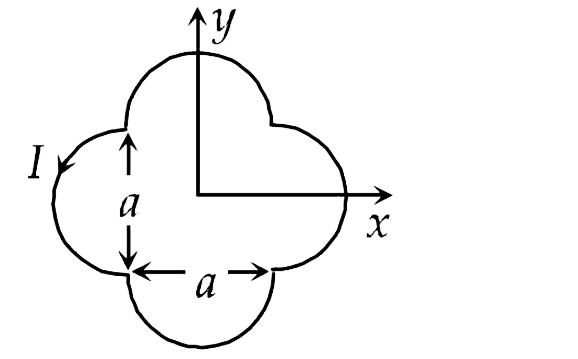
View SolutionA spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For a<<R the magnitude of the work done in the process is given by (4πpoRa2)X. where X is a a constant and y=Cp/Cv=41/30. The value of X is
View SolutionPut a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
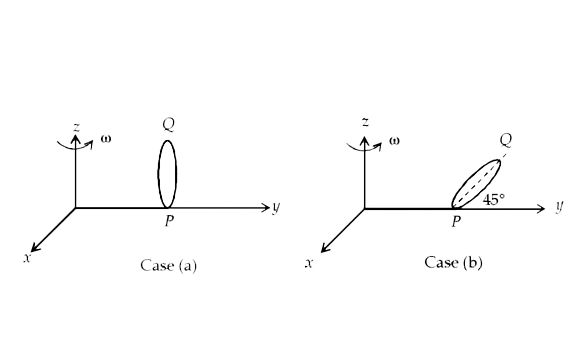
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same mass m and having velocity of 2omegaR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same angular velocity mass m and moving horizontally with velocity 2omegaR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
View SolutionTwo thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
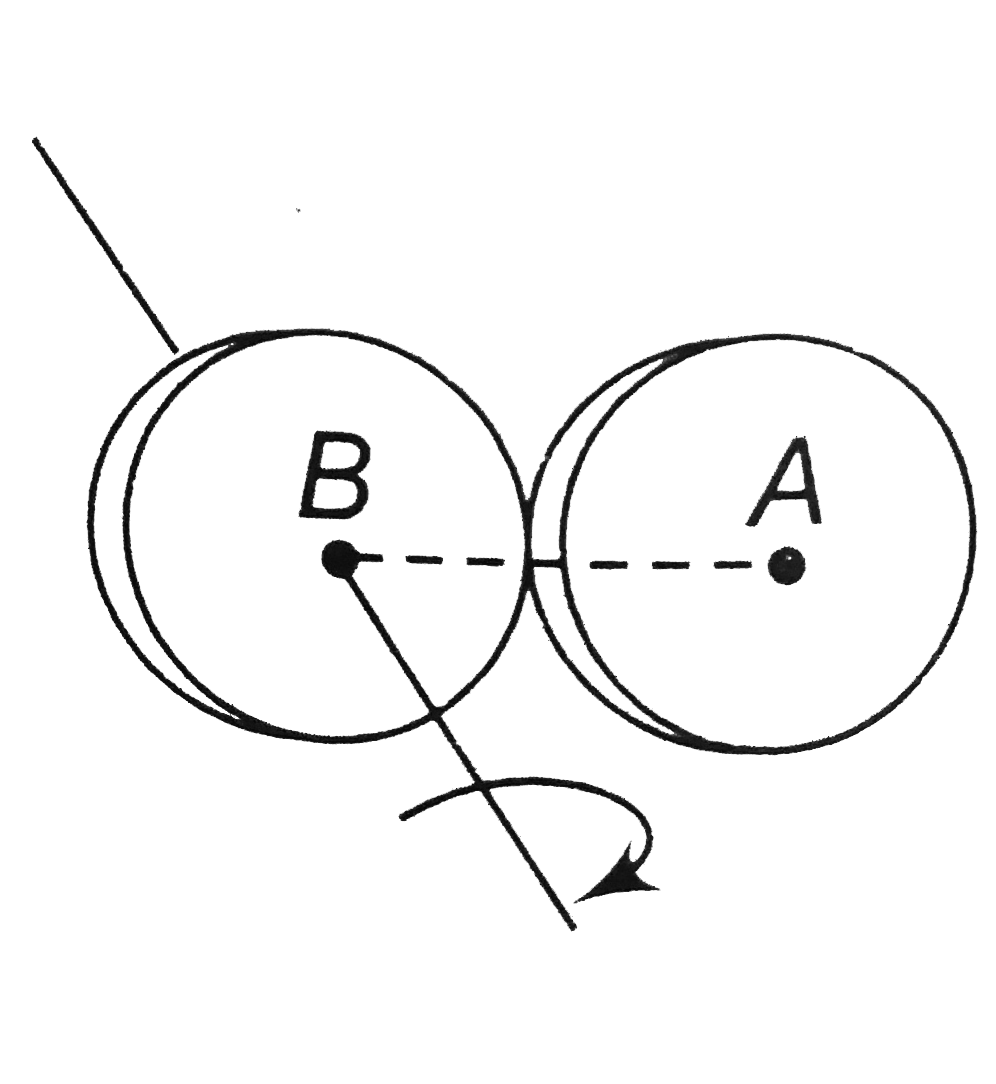 .
.
View SolutionThe mass of a body cannot be considered to be concentrated at the centre of mass of the body for the purpose of computing its moment of inertia.
For then the moment of inertia of every body about an axis passing through its centre of mass would be zero.
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about. (a) axis 'AB' ( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc (b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
View SolutionTwo thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
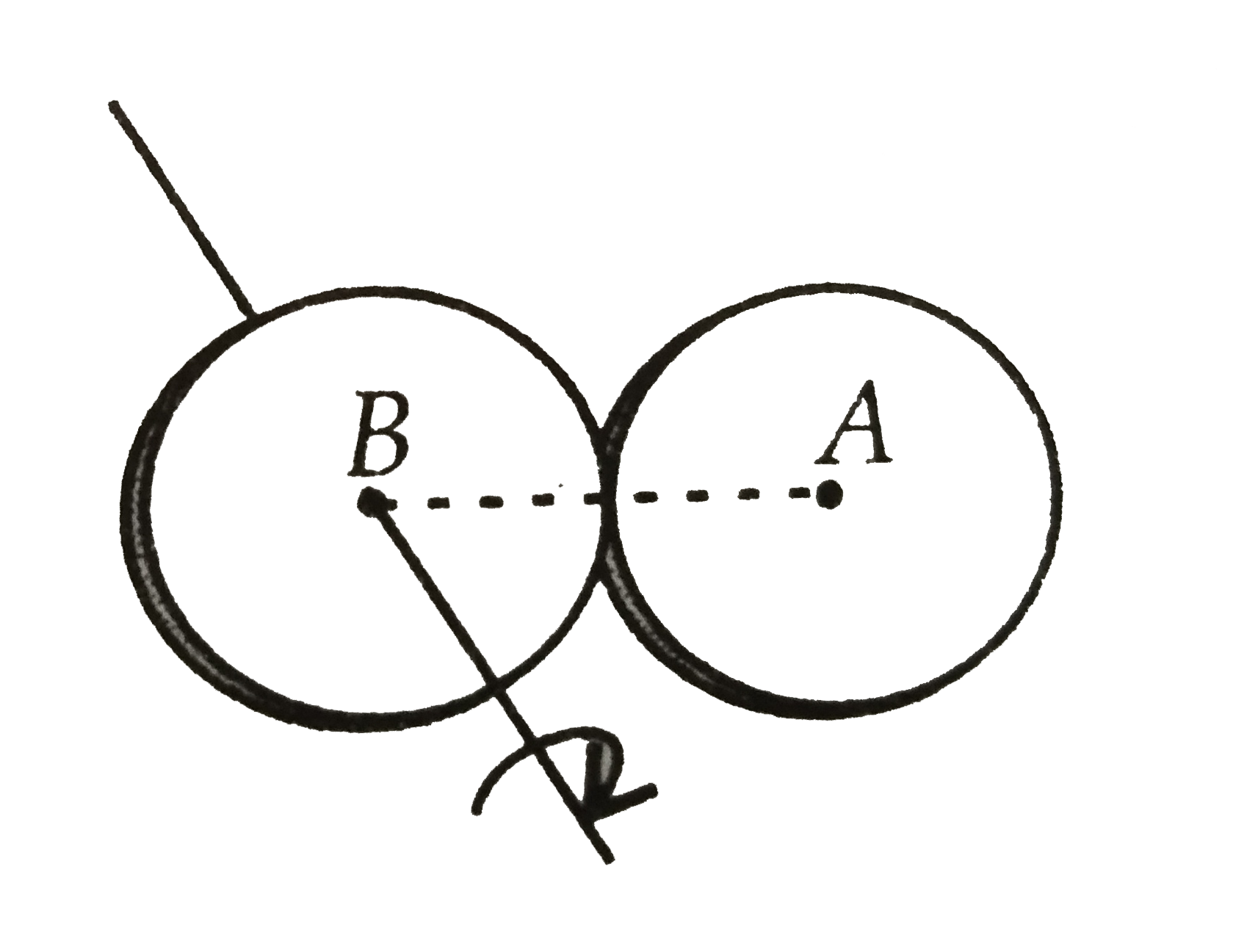
View SolutionM.I. of a thin uniform circular disc about one of the diameters is I. Its M.I. about an axis perpendicular to the plane of disc and passing through its centre is
View SolutionThe moment of inertial of a thin circular disc about an axis passing through its centre and perpendicular to its plane is I. Then, the moment of inertia of the disc about an axis parallel to its diameter and touching the edge of the rim is
View SolutionIn pure rolling motion of a ring (a) it rotates about instantaneous point of contact of ring and ground (b) its centre of mass moves in translatory motion only (c ) its centre of mass will have translatory as well as rotatory motion
View SolutionIn pure rolling motion of a ring (a) it rotates about instantaneous point of contact of ring and ground (b) its centre of mass moves in translatory motion only (c) its centre of mass will have translatory as well as rotatory motion
View Solution
