Two identical uniform discs roll without slipping on tow different sufaces AB and CD (see figure) starting at A and C with linear speeds v1andv2 respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed v1=3m/sthenv2∈m/sis(g=10m/s2)
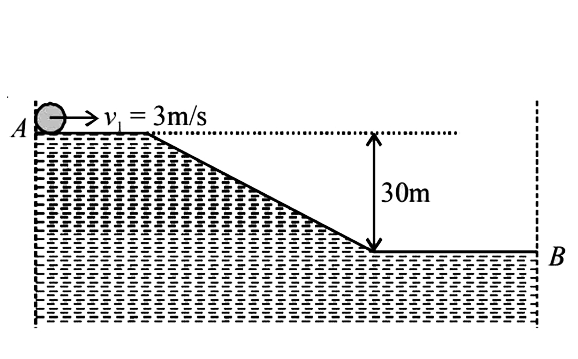

Step by step video & image solution for Two identical uniform discs roll without slipping on tow different sufaces AB and CD (see figure) starting at A and C with linear speeds v_1 and v_2 respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed v_1= 3m//s then v_2 in m//s is (g = 10 m//s^2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Section-2
10 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - SECTION -1
8 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - SECTION -3 (MATCHING LIST TYPE)
3 Videos
- JEE (ADVANCE) 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 3
6 Videos
- JEE ADVANCED 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-3
6 Videos
Similar Questions
Knowledge Check
A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)Two identical photo-cathodes receive light of frequencies v1 and v2. If the velocities of the photoelectrons (of mass m) coming out are v1 and v2 respectively, then
Av1−v2=[(2hm)(v1−v2))]1/2Bv21−v22=2hm(v1−v2)Cv1−v2=[(2hm)(v1−v2))]1/2Dv21−v22=2hm(v1−v2)Two identical cylinders roll from rest on two identical planes of slant lengths s and 2s but of the same height h. Then, the velocities, v1 and v2 acquired by the cylinders when they reach the bottom of the incline are related as.
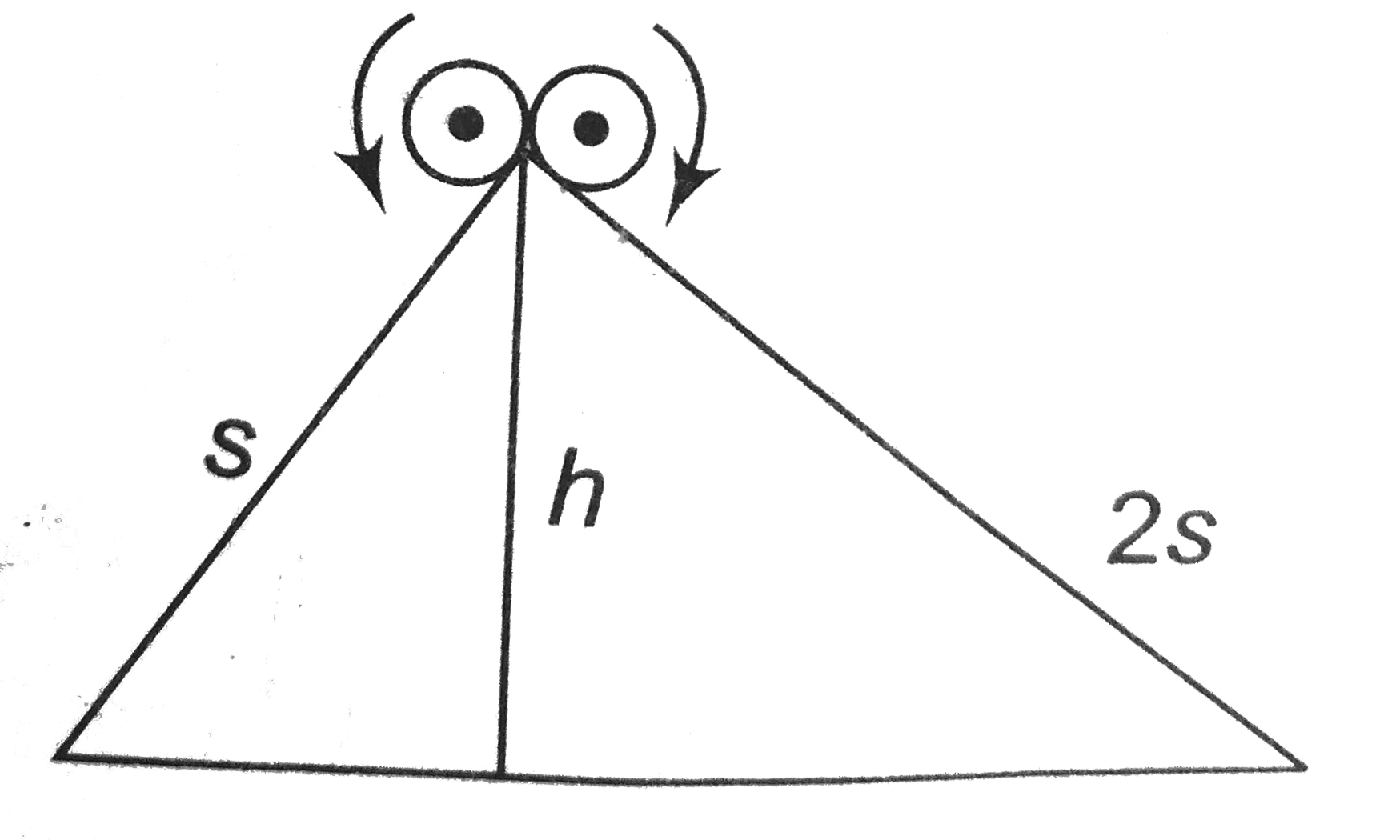 .Av1=v2Bv1=2v2C2v1=v2DNone of the above.
.Av1=v2Bv1=2v2C2v1=v2DNone of the above.

Particle P shown in figure is moving in a circle of radius R=10 cm with linear speed v=2m/s Find the angular speed of particle about point O.
View SolutionWhat will be the reading of spring balance in the figure shown in following situations ( g=10m/s2 )
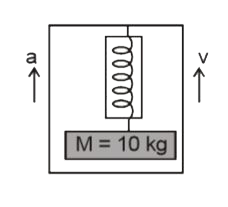
a=−2m/s2,v=0
View SolutionA wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is

View SolutionA small sphere of mass 1 kg is rolling without slipping with linear speed
v=√2007m/s

It leaves the inclined plane at point C.
Find the linear speed at point C.
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View Solution

