While conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S1,S2) emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane (forz>0) at a distance D=3 m from the mid-point of S1,S2, as shown schematically in the figure. The distance between the sources d=0.6003mm. The origin O is at the intersection of the screen and the line joining S1S2. Which of the following is (are) true of the intensity pattern of the screen?
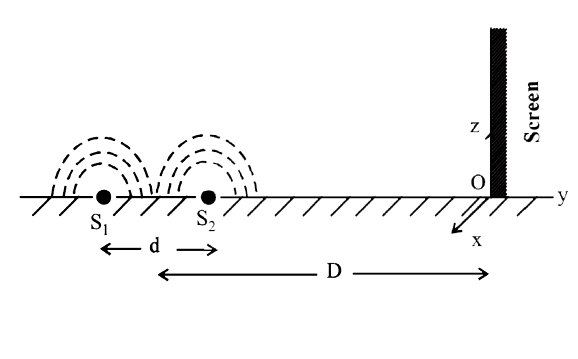
Straight bright and dark bands parallel to the x-axis
The region very close to the point O will be dark
Hyperbolic bright and dark bands with foci symmetrically placed about O in the x-direction
Semi circular bright and dark bands centered at point O
Step by step video & image solution for While conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S_(1),S_(2)) emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane (for zgt0) at a distance D=3 m from the mid-point of S_(1),S_(2), as shown schematically in the figure. The distance between the sources d=0.6003 mm. The origin O is at the intersection of the screen and the line joining S_(1)S_(2). Which of the following is (are) true of the intensity pattern of the screen? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Two coherent point sources S1 and S2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
View SolutionIn a Young's double slit experiment, a monochromatic source of wavelength λ is used to illuminate the two slits S1 and S2.
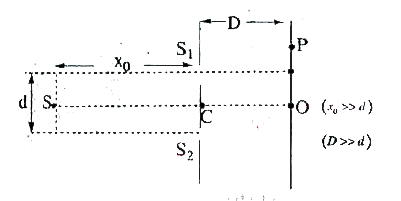
The slits S1 and S2 are identical and source S is placed symmetrical as shown. Interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
if the resultant intensity at P is same as that O, then the distance OP cannot be
View SolutionIn a Young's double slit experiment, a monochromatic source of wavelength λ is used to illuminate the two slits S1 and S2.

The slits S1 and S2 are identical and source S is placed symmetrical as shown. Interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
if the source is moved by up by a very small distance y0, the central maxima will shift
View SolutionIn a Young's double slit experiment, a monochromatic source of wavelength λ is used to illuminate the two slits S1 and S2.

The slits S1 and S2 are identical and source S is placed symmetrical as shown. Interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the size of slit S1 is slightly decreased, then
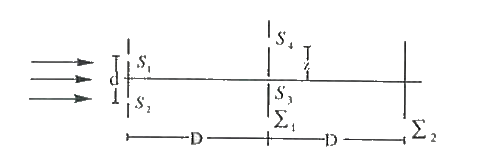
View SolutionConsider the situation shown in figure , The two slits S1andS2 placed symmetrically around the central line are illumated by a monocharmotic by a monocharomatic light of wavelength λ . The separation between the slits is d . The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits . The slit S3 is at the central line and the slit S4 is at a distance z from S3 .Another screen Σ2 is placed a further distance D away from Σ1 .Find the ratio of the minimum intensity observed on Σ2 if z is equal to
(1) z=λD2d
(2) λDd
(3) λD4d
View SolutionIn a Young.s double slit experiment , a monochromatic source if wavelength lambda is used to illmunate the two slits S_(1) and S_(2) The slits S_(1)and S_(2) are identical and source S is placed symmetrically as shown .Interference pattern is observed on a screen at a distance D from the centre of slit . The distance between the slits is d .If the size of slit S_(1) is slightly decreased , them
View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
View Solution
