What is the fundamental difference between an relation and a function? Is every relation a function?
To answer the question regarding the fundamental difference between a relation and a function, we can break down the concepts step by step.
1. Definition of Relation:
- A relation is a set of ordered pairs that connects elements from two sets. For example, if we have two sets A and B, a relation can be represented as a set of pairs (a, b) where 'a' is from set A and 'b' is from set B.
2. Example of a Relation:
- Consider two sets:
- Set A = {-1, 0, 1, 2}
- Set B = {2, 3, 4, 5}
- A possible relation can be: R = {(-1, 2), (-1, 3), (0, 4), (1, 5)}.
- Here, the input -1 relates to two outputs (2 and 3), which illustrates that a relation can have multiple outputs for a single input.
3. Definition of Function:
- A function is a specific type of relation where each input is associated with exactly one output. This means that for every element in set A, there is a unique corresponding element in set B.
4. Example of a Function:
- Using the same sets A and B, a valid function could be:
- F = {(-1, 2), (0, 3), (1, 4), (2, 5)}.
- In this case, each input from set A has a unique output in set B. For instance, -1 relates only to 2, 0 relates only to 3, and so on.
5. Fundamental Difference:
- The fundamental difference between a relation and a function is that while a relation can have multiple outputs for a single input, a function must have exactly one output for each input. Therefore, every function is a relation, but not every relation is a function.
6. Conclusion:
- To answer the second part of the question: No, not every relation is a function. A relation can fail to be a function if it associates an input with more than one output.
- A relation is a set of ordered pairs that connects elements from two sets. For example, if we have two sets A and B, a relation can be represented as a set of pairs (a, b) where 'a' is from set A and 'b' is from set B.
- Consider two sets:
- Set A = {-1, 0, 1, 2}
- Set B = {2, 3, 4, 5}
- A possible relation can be: R = {(-1, 2), (-1, 3), (0, 4), (1, 5)}.
- Here, the input -1 relates to two outputs (2 and 3), which illustrates that a relation can have multiple outputs for a single input.
- A function is a specific type of relation where each input is associated with exactly one output. This means that for every element in set A, there is a unique corresponding element in set B.
- Using the same sets A and B, a valid function could be:
- F = {(-1, 2), (0, 3), (1, 4), (2, 5)}.
- In this case, each input from set A has a unique output in set B. For instance, -1 relates only to 2, 0 relates only to 3, and so on.
- The fundamental difference between a relation and a function is that while a relation can have multiple outputs for a single input, a function must have exactly one output for each input. Therefore, every function is a relation, but not every relation is a function.
- To answer the second part of the question: No, not every relation is a function. A relation can fail to be a function if it associates an input with more than one output.
Topper's Solved these Questions
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - EXERCISE 3B
8 Videos
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - EXERCISE 3C
15 Videos
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - SOLVED EXAMPLES
20 Videos
- ELLIPSEBOOK - RS AGGARWALCHAPTER - ELLIPSEEXERCISE - EXERCISE
26 Videos
- GEOMETRICAL PROGRESSIONBOOK - RS AGGARWALCHAPTER - GEOMETRICAL PROGRESSIONEXERCISE - EXERCISE 12H (Very Short Answer Type Questions)
13 Videos
Similar Questions
Consider the following statements in respect of relations and functions:
1. All relations are functions but all functions are not relations.
2. A relation from A to B is a subset of Cartesian product A x B.
3. A relation in A is a subset of Cartesian product A x A.
Which of the above statements are correct?
View SolutionRelation and function Handwritten Notes
View Solution
Knowledge Check
What is fundamental function of Centriole in a cell?
AProtein synthesisBnucleolus formationCcell-wall formationDcell division initiationWhich of the following relation is a function ?
A{(a,b) (b,e)(c,e) (b,x)}B{(a,d)(a,b)(b,e)(a,b)}C{(a,d)(b,e)(c,d)(e,x)}D{(a,b)(b,m)(b,y)(d,x)}Which of the following relation is a function ?
A{(1, 4), (2, 6), (1, 5), (3, 9)}B{(3,3), (2, 1), (1,2), (2, 3)}C{(1, 2), (2,2),(3,2), (4,2)}D{(3, 1), (3,2), (3,3), (3, 4)}
Relation between graphs of a function and its inverse
View SolutionDefinition OF relation and function domain and range
View SolutionRelation between domain and function of composite functions
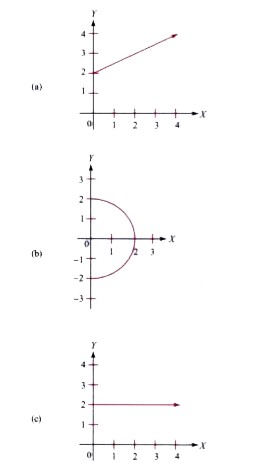
View SolutionThe diagrams given below represent relations from X to Y. Classify them as relation or function. If the relation is a function, classify it as one - one or many - one.
View SolutionIdentify the diagram and related function

View Solution
