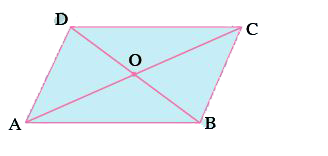
ABCD is a parallelogram. The diagonals AC and BD intersect each other at ‘O’. Prove that ar(ΔAOD)=ar(ΔBOC) . (Hint: Congruent figures have equal area)
 Solution in Bengali
Solution in Bengali
Step by step video & image solution for ABCD is a parallelogram. The diagonals AC and BD intersect each other at ‘O’. Prove that ar(DeltaAOD) = ar(DeltaBOC) . (Hint: Congruent figures have equal area) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS BOOK - NCERT BANGLISHCHAPTER - AREAS EXERCISE - EXERCISE 11.2
9 Videos
- AREAS BOOK - NCERT BANGLISHCHAPTER - AREAS EXERCISE - EXERCISE 11.3
9 Videos
- AREAS BOOK - NCERT BANGLISHCHAPTER - AREAS EXERCISE - THINK, DISCUSS AND WRITE
4 Videos
- CIRCLESBOOK - NCERT BANGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 12.5
5 Videos
Similar Questions
The area of parallelogram ABCD is 36cm2 . Calculate the height of parallelogram ABEF if AB = 4.2 cm
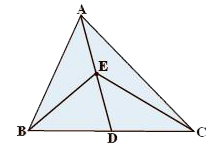
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
View SolutionIf 1cm represents 5m, what would be an area of 6 square cm. represent ?
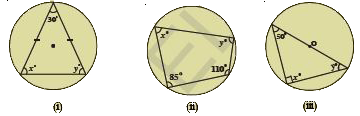
View SolutionFind the values of x and y in the figures given below
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionएक चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(ΔAOD)=ar(ΔBOC) है । सिद्ध करों कि ABCD एक समलम्ब है।
View Solution
