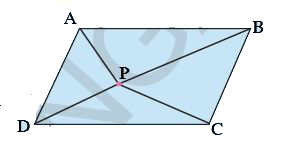
P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (ΔAPB)+ar(ΔPCD)=12ar(ABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)
(Hint : Throught , P draw a line parallel to AB)
 Solution in Bengali
Solution in Bengali
Step by step video & image solution for P is a point in the interior of a parallelogram ABCD. Show that (i) ar (DeltaAPB) +ar (DeltaPCD)=1/2ar (ABCD) (ii) ar(DeltaAPD)+ar (DeltaPBC)=ar(DeltaAPB)+ar(DeltaPCD) (Hint : Throught , P draw a line parallel to AB) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
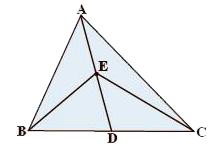
In a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
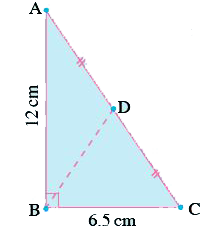
View SolutionIn ΔABC,∠ABC=90∘,AD=DC,AB=12cmandBC=6.5 cm. Find the area of ΔADB .
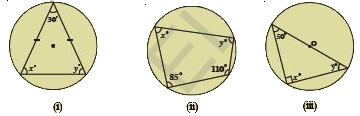
View SolutionFind the values of x and y in the figures given below
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
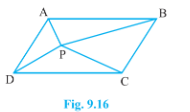
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionIn the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
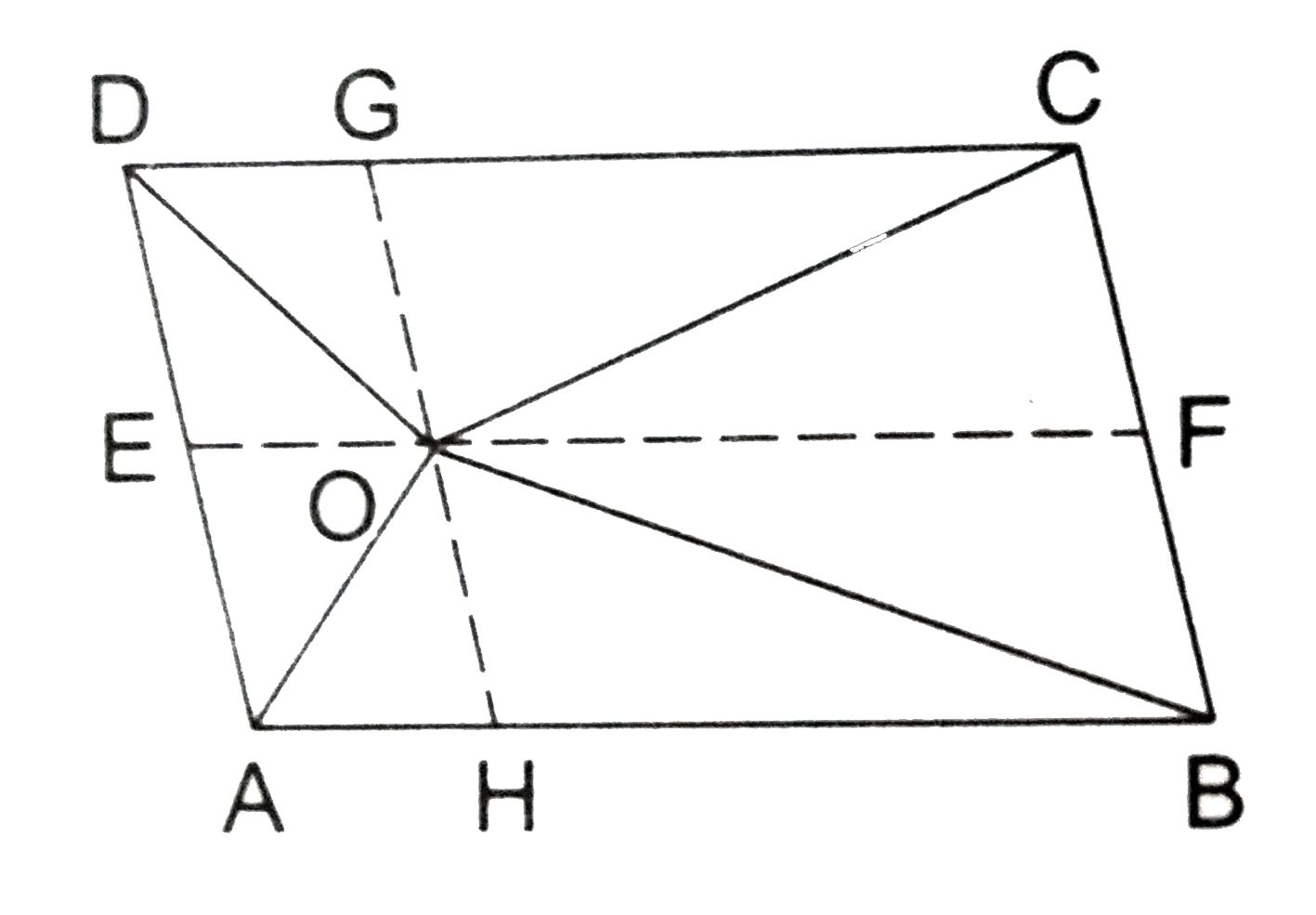
View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
View Solutionदिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की
(i)ar(APB)+ar(PCD)=12ar(ABCD)
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View SolutionIn P is a point in the interior of a parallelogram ABCD. Show that<br>(ii)ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
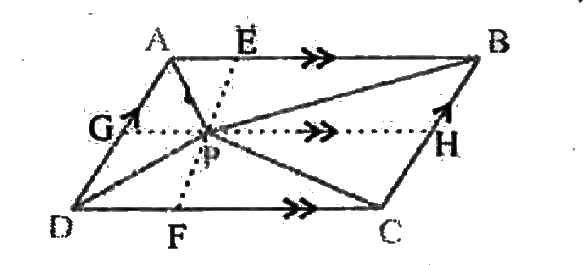
View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = 12 ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View SolutionIn the figure ''P'' is a point in the interior of a parallelogram ABCD.
Show that area of ΔAPD+ area of ΔPBC = area of ΔAPB+ area of ΔPCD.
View Solutionआकुति में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है दर्शाइए कि
Ar (APB ) + ar (PCD)=12ar(ABCD)
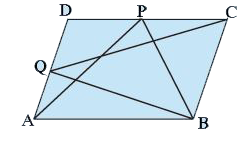
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD show that ar(ΔAPB)=arΔ(BQC)
View Solution
