A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig.) . A uniform magnetic field extends over a circular region within the rim. It is given by,
B=−B0K(r≤a,a<R)=0(otherwise)

−Bπa2λMRˆk
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT BANGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISES
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - NCERT BANGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - EXERCISES
29 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT BANGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ADDITIONAL EXERCISES
5 Videos
Similar Questions
A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig. 6.22). A uniform magnetic field extends over a circular region within the rim. It is given by,
B=B0k (ra≤a,a<R)
=0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off?

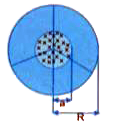
View SolutionA line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig. 6.08). A uniform magnetic field extends over a circular region within the rim. It is given by,
→B=−B0ˆk(r≤a,aItR)
= 0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off ?
View Solution
Knowledge Check
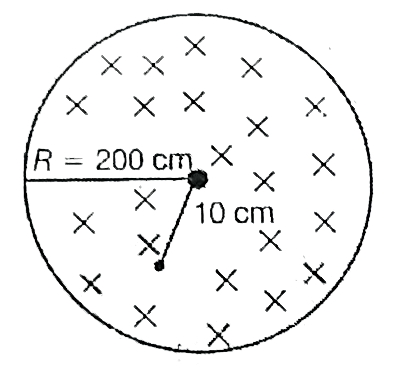
A line charge λ per unit length is pasted uniformly on to the wire of a wheel of mass m and radius R. The wheel has light non-conducting spokes and is free to rotate about a vertical axis as shown in Fig.3.166. A uniform magnetic field extends over a radial rigion of radius r given by B=−B0ˆk(r≤a,a<R)=0 (otherwise). What is the angular velocity of the wheel this field is suddenly switched off?
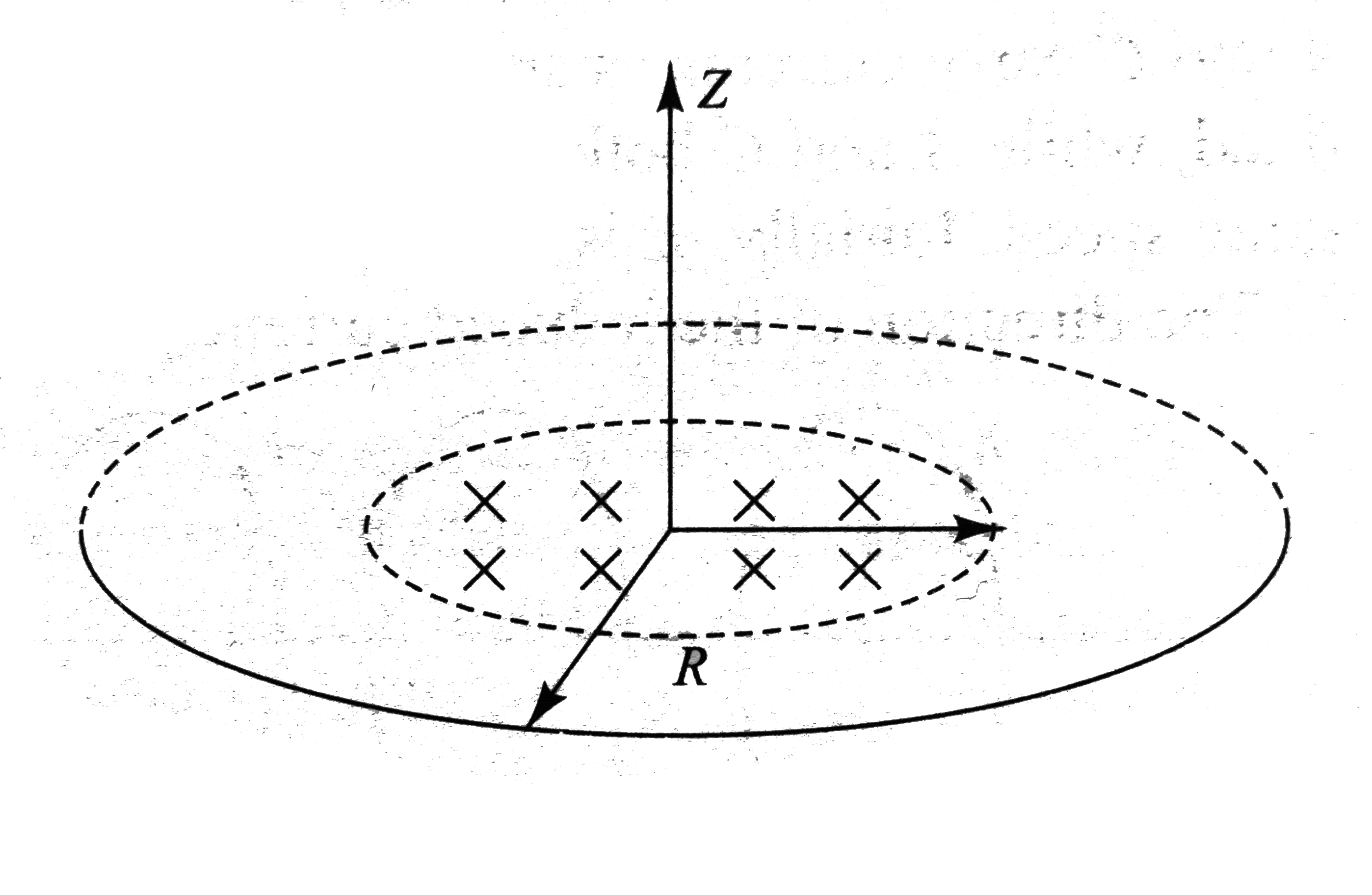 A(a) −2B0πa2rmRˆkB(b) −2B0πa2r3mRˆkC( c) B0πa2λmRˆkD( d) −B0πa2λmRˆk
A(a) −2B0πa2rmRˆkB(b) −2B0πa2r3mRˆkC( c) B0πa2λmRˆkD( d) −B0πa2λmRˆkA non-conducting ring of radius r has charge per unit length λ. A magnetic field perpendicular to plane of the ring changes at rate Db/dt. Torque experienced by the ring is
 Aλπr3dBdtBλ2πr3dBdtCλ2(2πr)2dBdtDzero
Aλπr3dBdtBλ2πr3dBdtCλ2(2πr)2dBdtDzeroA conducting solid sphere having uniform charge Q on it has radius R. It is rotating with anangular velocity ω. If a uniform magnetic field B is present perpendicular to axis of rotation then the torque on sphere will be
AqωR25BBqωR23RCqωR24BDqωR22R
A line charge λ per unit length is pasted uniformly on to the wire of a wheel of mass m and radius R. The wheel has light non-conducting spokes and is free to rotate about a vertical axis as shown in Fig.3.166. A uniform magnetic field extends over a radial rigion of radius r given by B=−B0ˆk(r≤a,a<R)=0 (otherwise). What is the angular velocity of the wheel this field is suddenly switched off?
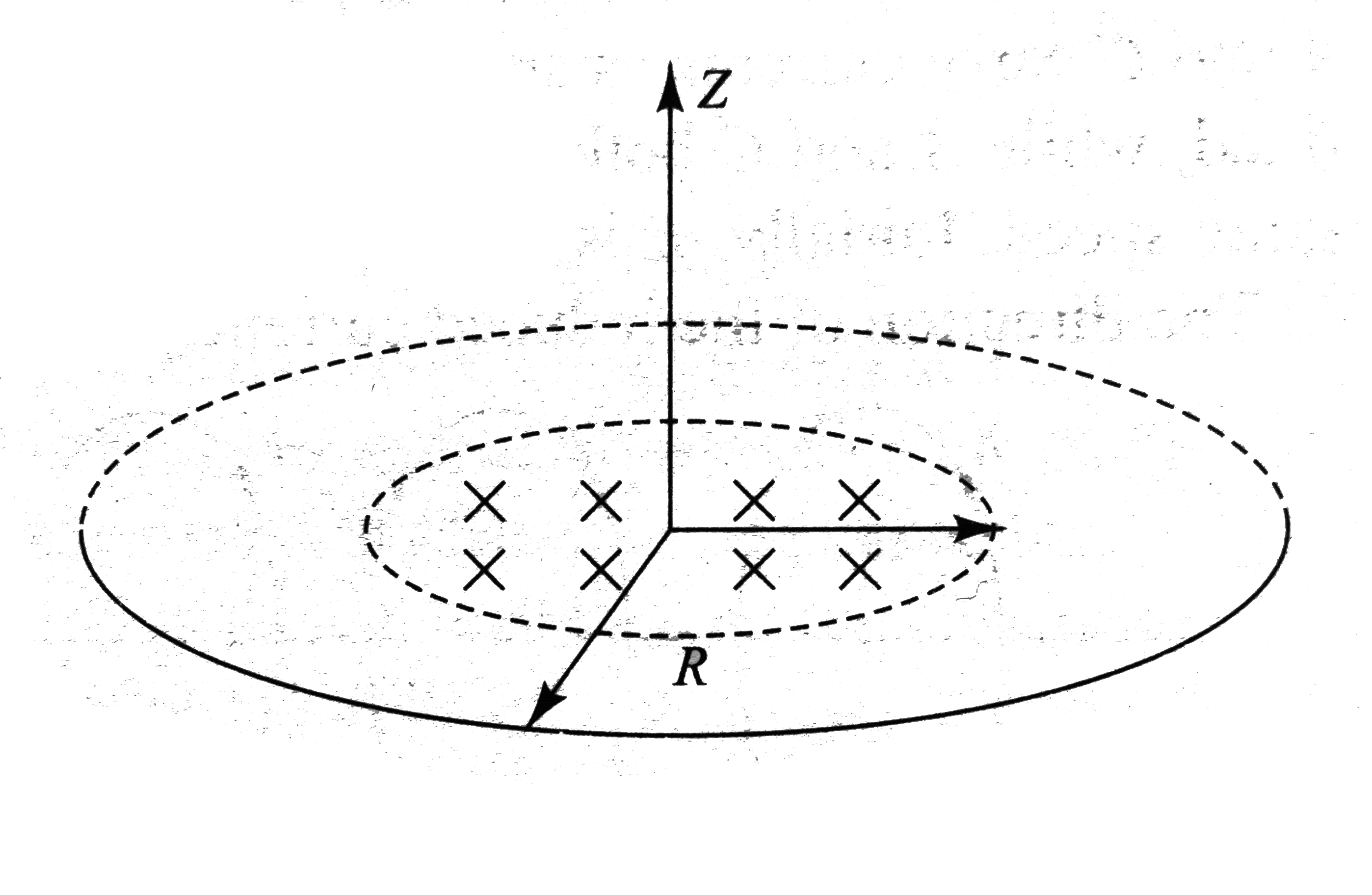
View SolutionA plastic disc of radius 'R' has a charge 'q' uniformly distributed over its surface. If the dis is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA plastic disc of radius 'R' has a charge 'q ' uniformly distributed over its surface. If the disc is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA bicycle wheel of radius 0.3 m has a rim of mass 1.0 kg and 50 spokes, each of mass 0.01 kg. What is its moment of inertia about its axis of rotation ?
View SolutionA bicycle wheel of radius 0.3 m has a rim of mass 1.0 kg and 50 spokes, each of mass 0.01 kg. What is its moment of inertia about its axis of rotation ?
View Solution
