Length of the fence of a trapezium shaped field ABCD is 120m. If BC=48m,CD=17mandAD=40m, find the area of this field. Side AB is perpendicular to the parallel sides ADandBC.
To find the area of the trapezium-shaped field ABCD, we can follow these steps:
Step 1: Identify the dimensions of the trapezium
Given:
- Length of the fence (perimeter) = 120 m
- BC (one of the parallel sides) = 48 m
- CD (the other parallel side) = 17 m
- AD (the non-parallel side) = 40 m
- AB is perpendicular to AD and BC.
Step 2: Find the length of side AB
Since AB is perpendicular to both parallel sides AD and BC, we can use the perimeter to find the length of side AB (let's denote it as h).
The perimeter of trapezium ABCD can be expressed as:
AB+BC+CD+AD=120
Substituting the known values:
h+48+17+40=120
Now, simplify the equation:
h+105=120
Subtract 105 from both sides:
h=120−105
h=15 m
Step 3: Calculate the area of the trapezium
The area A of a trapezium can be calculated using the formula:
A=12×(b1+b2)×h
where b1 and b2 are the lengths of the parallel sides, and h is the height.
Here, b1=BC=48 m, b2=CD=17 m, and h=15 m.
Substituting the values into the area formula:
A=12×(48+17)×15
A=12×65×15
A=9752
A=487.5 m2
Final Answer
The area of the trapezium-shaped field ABCD is 487.5 m2.
---
Given:
- Length of the fence (perimeter) = 120 m
- BC (one of the parallel sides) = 48 m
- CD (the other parallel side) = 17 m
- AD (the non-parallel side) = 40 m
- AB is perpendicular to AD and BC.
Since AB is perpendicular to both parallel sides AD and BC, we can use the perimeter to find the length of side AB (let's denote it as h).
AB+BC+CD+AD=120
Substituting the known values:
h+48+17+40=120
Now, simplify the equation:
h+105=120
Subtract 105 from both sides:
h=120−105
h=15 m
The area A of a trapezium can be calculated using the formula:
A=12×(b1+b2)×h
where b1 and b2 are the lengths of the parallel sides, and h is the height.
A=12×(48+17)×15
A=12×65×15
A=9752
A=487.5 m2
The area of the trapezium-shaped field ABCD is 487.5 m2.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - MENSURATIONEXERCISE - SOLVED EXAMPLES11videos
MENSURATION
- BOOK - NCERTCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.310videos
MENSURATION
- BOOK - NCERTCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - EXERCISE 2.39videos
LINEAR EQUATIONS IN ONE VARIABLE
- BOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - SOLVED EXAMPLES8videos
PLAYING WITH NUMBERS
Similar Questions
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC=48 m, CD=17 m and AD=40 m, find the area of this field. Side AB is perpendicular to the parallel sides ADandBC.
 View Solution
View SolutionLength of the fence of a trapezium shaped field ABCD is 120m. If BC=48m,CD=17mandAD=40m, find the area of this field. Side AB is perpendicular to the parallel sides ADandBC.
View Solution
Knowledge Check
- Question 1 - Select One
ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘ - Question 2 - Select One
The parallel sides of a trapezium field are 12 m and 20 m. If distance between the parallel sides is 8 m, find the area of the field.
A128 sqmB132 sq mC130 sq mD135 sq m - Question 3 - Select One
The parallel sides of trapezium field are 12 m and 20 m . If distnace between the parallel sides is 8 m, find the area of the field
A128 sq mB132 sq mC130 sq mD135 sq m
The length of the fence of a trapezium-shaped field ABCD is 120 m. IF BC=48m,CD=17mandAD=40m, then find the area of this field. Side AB is perpendicular to parallel sides ADandBC.
View SolutionThe length of the fence of a trapezium - shaped field ABCD is 130 m and side AB is perpendicular to each of the parallel sides AD and BC. If BC = 54 m, CD = 19 m and AD = 42 m, find the area of the field.
 View Solution
View SolutionThe area of a trapezium shaped field is 480 m2, the distance between two parallel sides is 15 m and one of the parallel side is 20 m. Find the other parallel side.
View SolutionIn the given figure ABCD is a trapezium in which AB = 40 m, BC=15 m ,CD= 28 m ,AD=9 m and CE⊥AB. area of trap.ABCD is
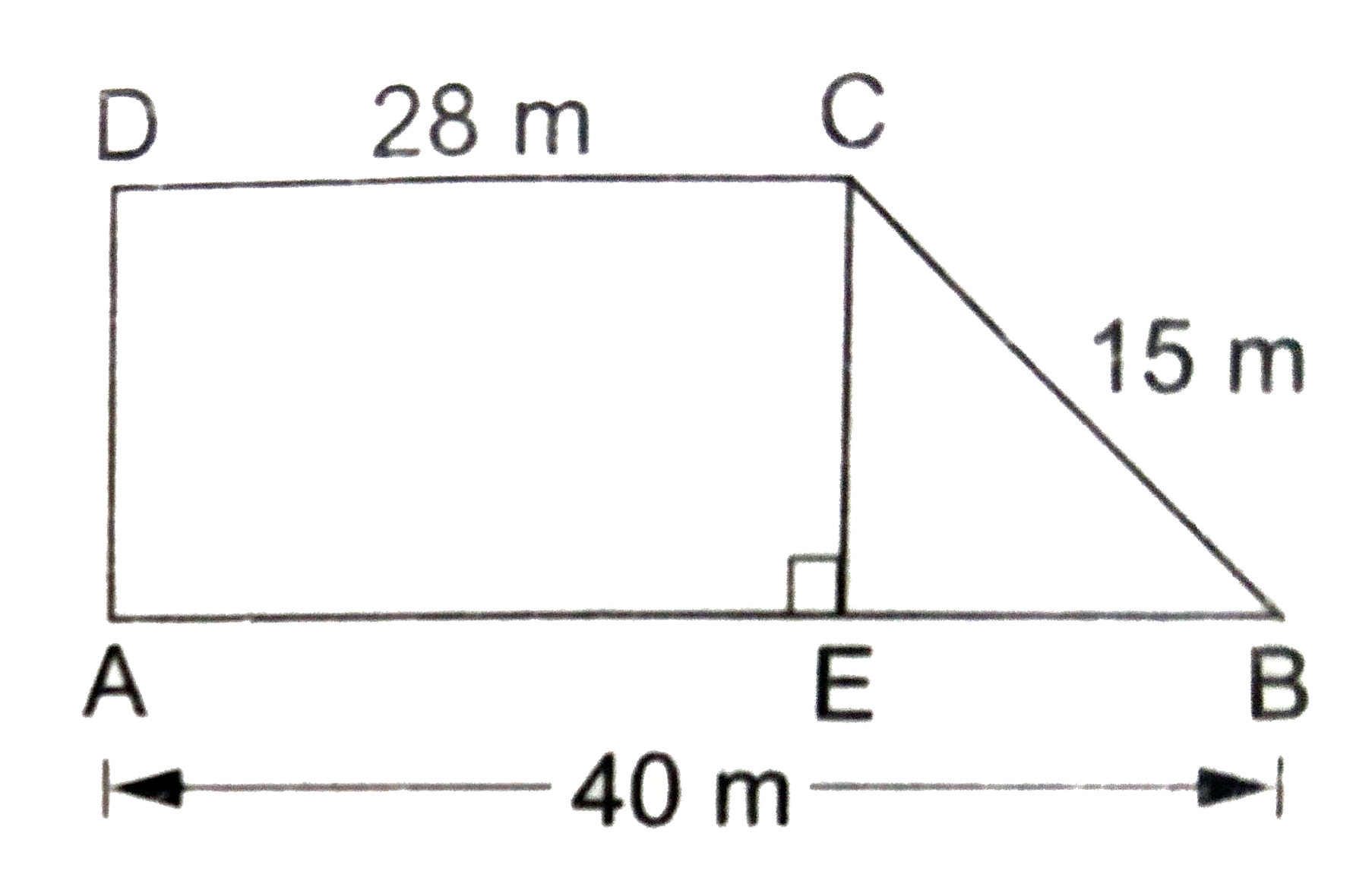 View Solution
View SolutionIn a trapezium-shaped field, one of the parallel sides is twice the other. If the area of the field is 9450m2 and the perpendicular distance between the two parallel sides is 84 m, find the length of the longer of the parallel sides.
View Solution

