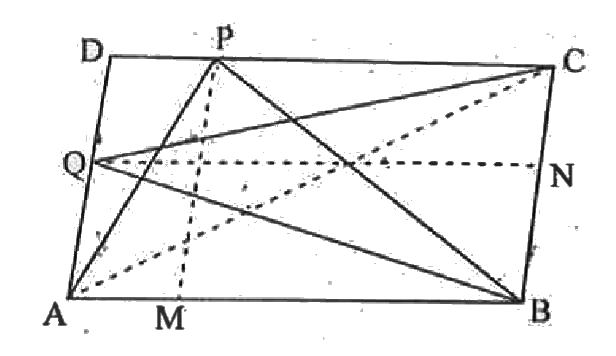
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
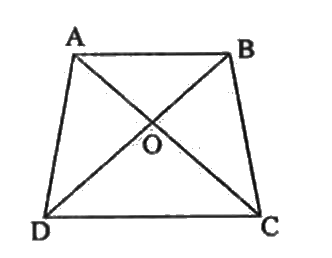
Diagonals AC and BD of a trapezium ABCD with AB∣∣DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
 03:46View Solution
03:46View SolutionIf 1cm represents 5m, what would be an area of 6 square cm. represent ?
02:11View SolutionGiven that the vertices A, B, C of a quadrilateral ABCD lie on a circle. Also ∠A+∠C=180∘ , then prove that the vertex D also lie on the same circle.
02:45View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogramABCD. Show that ar (APB) = ar (BQC).
02:17View SolutionDetermine the point of symmetry of a regular hexagon.
05:41View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionThe inequation represented by the graph given below is :
04:38View SolutionThe inequation that best describes the graph given below is _________
05:04View SolutionThe inequation that best describes the following graph is _________
03:22View SolutionP और Q क्रमश : समांतर चतुर्भुज ABCD कि भुजाओ में DC और AD पर स्थित बिंदु है । दर्शाइए कि ar(APB)=ar(BQC) है |
05:01View SolutionP और Q क्रमशः समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर बिन्दु है। दर्शाइए कि ar (APB) = ar (BQC) है।
03:51View SolutionP और Q किसी समांतर चतुर्भुज ABCD की भुजाओं DC तथा AD पर स्थित दो बिंदु है |दिखाएँ की ar(ΔAPB)=ar(ΔBQC)
04:38View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
 03:27View Solution
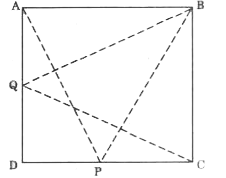
03:27View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram , ABCD . Show that ar(APB) = ar (BQC)
 03:22View Solution
03:22View Solution

