Go back to Pascal's triangle.
Line 1:1=11∘
Line 2:1,1=111
Line 3:1,2,1=112
Make a conjecture about Line 4 and Line 5. Does your conjecture hold ? Does your conjecture hold for Line 6 too ? Solution in Kannada
Step by step video & image solution for Go back to Pascal's triangle. Line 1 : 1 = 11^(@) Line 2 : 1, 1 = 11^(1) Line 3 : 1, 2, 1 = 11^(2) Make a conjecture about Line 4 and Line 5. Does your conjecture hold ? Does your conjecture hold for Line 6 too ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROOFS IN MATHEMATICSBOOK - NCERT KANNADCHAPTER - PROOFS IN MATHEMATICSEXERCISE - EXERCISE - 15.4
15 Videos
- PROOFS IN MATHEMATICSBOOK - NCERT KANNADCHAPTER - PROOFS IN MATHEMATICSEXERCISE - EXERCISE - 15.2
5 Videos
- PROBABILITY BOOK - NCERT KANNADCHAPTER - PROBABILITY EXERCISE - DO THIS
3 Videos
- QUADRILATERALSBOOK - NCERT KANNADCHAPTER - QUADRILATERALSEXERCISE - EXERCISE - 8.4
6 Videos
Similar Questions
State which of the following are mathematical statements and which are not? Give reason.
She has blue rays
View SolutionUse deductive reasoning to answer the following:
Human beings are mortal. Jeevan is a human being. Based on these two statements, what can you conclude about Jeevan ?
View SolutionToss a coin for number of times as shown in the table. And record your findings in the table.

What happens if you keep on increasing the number of tosses.
View SolutionABC is a triangle . D is a point of AB such that AD=14ABandE is a point on AC such that AE=14AC. If DE=2cm find BC.
View SolutionThe prejection of the line segment joining the poing (1,−1,3) and (2,−4,11) on the line joining the points (−1,2,3) and (3,−2,10), is ……
View SolutionEquations of the line through (4,−5,6) and perpendicular to the lines x−111=y+6−3=z−50and x−15=y−22=z−811 are
View SolutionGo back to Pascal's triangle.
Line 1:1=11∘
Line 2:1,1=111
Line 3:1,2,1=112
Make a conjecture about Line 4 and Line 5. Does your conjecture hold ? Does your conjecture hold for Line 6 too ?
View SolutionLook at the following pattern :
12=1
112=121
1112=12321
11112=1234321
111112=123454321
Make a conjecture about each of the following :
1111112=
11111112=
Check if your conjecture is true.
View SolutionNote the Pascal triangle: line 1: 1 = 11^@ Row 2: 11 = 11^1 Row 3: 121 = 11^2 Create hypotheses for line 4 and base line 5. Check whether these hypotheses are sustainable. Similarly to line 6, test your hypothesis.
View SolutionGo back to Pascal's triangle . Line -1 : 1=11^(0) Line -2 : 11 = 11^(1) Line-3 : 121 = 11^(2) Make a conjecture about Line-4 and Line-5 . Does your conjecture hold ? Does your conjecture hold for Line -6 too ?
View SolutionLook at the following pattern: 1^(2) = 1 11^(2) =121 111^2 = 12321 1111^(2)=1234321 11111^2 = 123454321 Make a conjecture about about each of the following : 111111^2=.............. 1111111^2=........... Check if your conjecture is true .
View SolutionGo back to Pascal's triangle . Line -1 : 1=11^(0) Line -2 : 11 = 11^(1) Line-3 : 121 = 11^(2) Make a conjecture about Line-4 and Line-5 . Does your conjecture hold ? Does your conjecture hold for Line -6 too ?
View SolutionLook at the following pattern: 1^(2) = 1 11^(2) =121 111^2 = 12321 1111^(2)=1234321 11111^2 = 123454321 Make a conjecture about about each of the following : 111111^2=.............. 1111111^2=........... Check if your conjecture is true .
View SolutionLook at the following pattern:
12=1
112=121
1112=12321
11112=1234321
111112=123454321
Make a conjecture about about each of the following :
1111112=..............
11111112=...........
Check if your conjecture is true .
View SolutionGo back to Pascal's triangle .
Line -1 : 1=110
Line -2 : 11=111
Line-3 : 121=112
Make a conjecture about Line-4 and Line-5 .
Does your conjecture hold ? Does your conjecture hold for Line -6 too ?
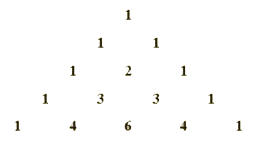
View SolutionLook at the following pattern:
12=1
112=121
1112=12321
11112=1234321
111112=123454321
Make a conjecture about about each of the following :
1111112=..............
11111112=...........
Check if your conjecture is true .
View Solution
