In trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF || AB. Show that AEED=BFFC
The correct Answer is:AEED=BFFC
Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - DO THIS (FILL IN THE BLANKS)
6 Videos
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - DO THIS TRUE /FALSE
5 Videos
- SETSBOOK - NCERT KANNADCHAPTER - SETSEXERCISE - Try This
11 Videos
- TANGENTS AND SECANTS TO A CIRCLEBOOK - NCERT KANNADCHAPTER - TANGENTS AND SECANTS TO A CIRCLEEXERCISE - Try this
3 Videos
Similar Questions
ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View Solution
Knowledge Check
ABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
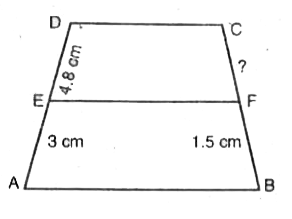 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of theseABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
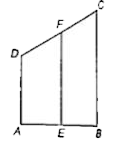 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
In a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
View SolutionABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
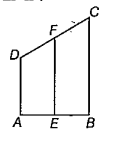
View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that :
PQ is parallel to AB.
View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP product meets CD produced at point E. Prove that :
Point P bisects BE,
View Solution
