Suppose the loop in Exercise 6.4 is stationary but the current feeding the electromagnet that produces the magnetic field is gradually reduced so that the field decreases from its initial value of 0.3 T at the rate of 0.02 Ts−1. If the cut is joined
Here ν = 0.5 Hz, N =100, A = 0.1 m2 and B = 0.01 T. Employing Eq.
Eq. (6.21)
ε0=NBA(2πv)
=100×0.01×0.1×2×3.14×0.5
=0.314V
The maximum voltage is 0.314 V
We urge you to explore such alternative possibilities for power generation.
Similar Questions
Suppose the loop in Q.4 is stationary, but the current feeding the electromagnet the produces the magnetic field is gradually reduced so that the field decreases form its initial value of 0.3 T at the rate of 0.2 T/sec. If the cut is joined and loop has a resistance of 1.6Ω, how much power is dissipated by the loop as heat ? What is the source of this power ?
View SolutionA rectangular loop of sides 10 cm and 5 cm with a cut is stationary between the pole pieces of an electromagnet.
The magnetic field of the magnet is normal to the loop. The current feeding the electromagnet is reduced, so that the field decreased from its initial value of 0.2 T at the rate of 0.02Ω. If the cut is joined and the loop has a resistance of 2.0Ω, then the power dissipated by the loop as heat is
View Solution
Knowledge Check
A rectangular loop of sides 10cm and 5cm with a cut is stationary between the pole pieces of an electromagnet. The amgnetic field of the magnet is normal to the loop. The current feeding the electromagnet is reduced so that the field decreases from its initial value of 3.0T at the rate of 0.02Ts−1. If the cut is joined and the loop has a resistance of 2.0Ω, the power dissipated by the loop as heat is
A(a) 5nWB(b) 4nWC( c) 3nWD(d) 2nWA rectangular loop of sides 10 cm and 5 cm with a cut is stationary between the pole pieces of an electromagnet.
The magnetic field of the magnet is normal to the loop. The current feeding the electromagnet is reduced, so that the field decreased from its initial value of 0.2 T at the rate of 0.02Ω. If the cut is joined and the loop has a resistance of 2.0Ω, then the power dissipated by the loop as heat isA5 nWB4 nWC3 nWD2 nWThe figure shows a uniform, 3.0 T magnetic field that is normal to the plane of a conducting, circular loop with a resistance of 1.5 Ω and a radius of 0.024 m. The magnetic field is directed out of the paper as shown . Note: The area of the non-circular portion of the wire is considered negligible compared to that of the circular loop.
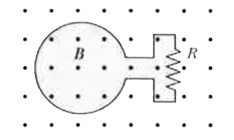
If the magnetic field is held constant at 3.0 T and the loop is pulled out of the region that contains the field in 0.2 s, at what rate is energy dissipated in R?A1.8×10−2WB3.8×10−3WC4.9×10−4WD2.7×10−4W
A rectangular loop of sides 8 cm and 2 cm with a small cut is stationary in a uniform magnetic field directed normal to the loop. The magneic field is reduced form its initial value of 0.3 T at the rate of 0.2 T s−1. If the cut is joined and the loop has a resistance of 1.6Ω, how much power is dissipated by the loop as heat ?
View SolutionA conducting circular loop is placed in a magnetic field of strength 0.04 T, such that the plane of the loop is perpendicular to the magnetic field. If the radius of the loop begins to shrink at a constant rate of 0.5mm/s, then calculate the emf induced in the loop when its radius is 1.5 cm.
View SolutionA current - carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of (6.0×10−5) T at its centre. Find the value of the current.
View SolutionA current - carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of (6.0×10−5) T at its centre. Find the value of the current.
View SolutionThe magnetic field at a distance r from a long wire carryimg current I is 0.4 T. The magnetic field at a distance 2r is
View Solution
