. Let A be the centre of the circle $x^{2} + y^{2} - 2 x - 4 y - 20 = 0$ Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD

Video Solution

Text Solution

Verified by Experts

The correct Answer is:75 sq. units

The equation of the circle is
$x^{2} + y^{2} - 2 x - 4 y - 20 = 0$
Center $\equiv (1, 2)$ radius $= \sqrt{1 + 4 + 20} = 5$
The equation of tangent at $(1, 7)$ is
$x .1 + y .7 - (x + 1) - 2 (y + 7) - 20 = 0$
or $y - 7 = 0$ (1)
Similarly, the equation of tangent at (4,-1) is
$4 x - 2 y - (x + 4) - 2 (y - 2) - 20 = 0$
or $3 x - 4 y - 20 = 0$ (2)

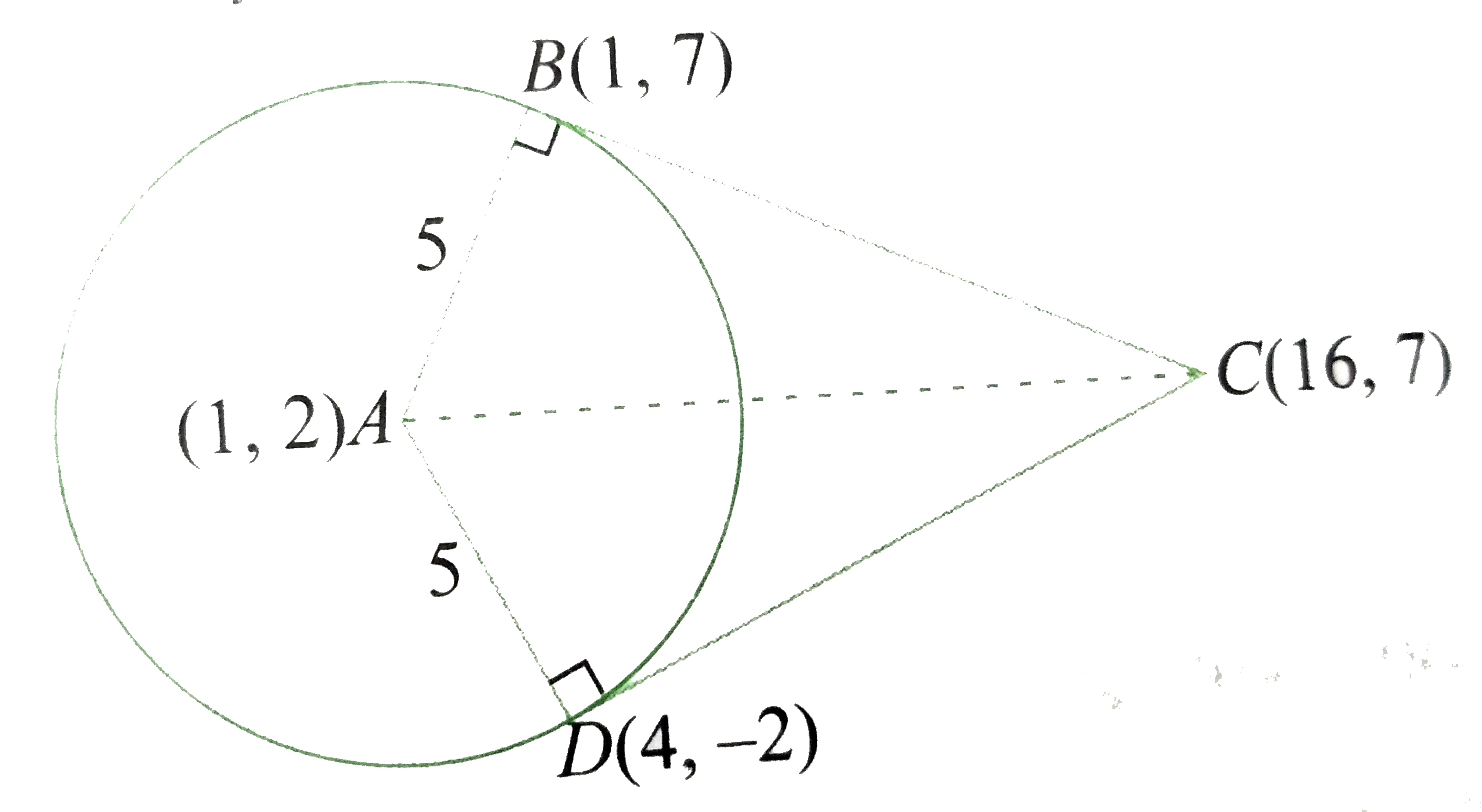
For point C, solving (1) and (2), we get $x = 16$ and $y = 7$ . Therefore, $C \equiv (16, 7)$
Now, clearly ,
ar(quad. BCDA) $= 2 \times$ ar ( $Δ A B C)$
$= 2 \times \frac{1}{2} \times A B \times B C$
$= A B \times B C$
where $A B =$ Radius of circle $= 5$
and $B C = 15$
$∴$ ar (quad. ABCD) $= 5 \times 15 = 75 s q .$ units

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let A be the centre of the circle $x^{2} + y^{2} - 2 x - 4 y - 20 = 0$ . If the tangents at the points B (1, 7) and $D (4, - 2)$ on the circle meet at the point C, then the perimeter of the quadrilateral ABCD is
A60 units
B20 units
C40 units
D50 units
Question 2 - Select One
Let A be the centre of the circle $x^{2} + y^{2} - 2 x - 4 y - 20 = 0$ .If the tangents at the points B(1,7)andD(4,-2) on the circle meet at C , then find the area of the quadrilateral ABCD .
A78
B75
C79
D85

CENGAGE-CIRCLE -Exercise 4.4

Home
Ask Doubt
Profile