Any circle through the point of intersection of the lines $x + \sqrt{3} y = 1$ and $\sqrt{3} x - y = 2$ intersects there lines at points $P a n d Q$ . Then the angle subtended by the are $P Q$ at its center is $180^{0}$ (b) $90^{0}$ (c) $120^{0}$ depends on center and radius

A

$180^{\circ}$

B

$90^{\circ}$

C

$120^{\circ}$

D

Depends on centre and radius

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

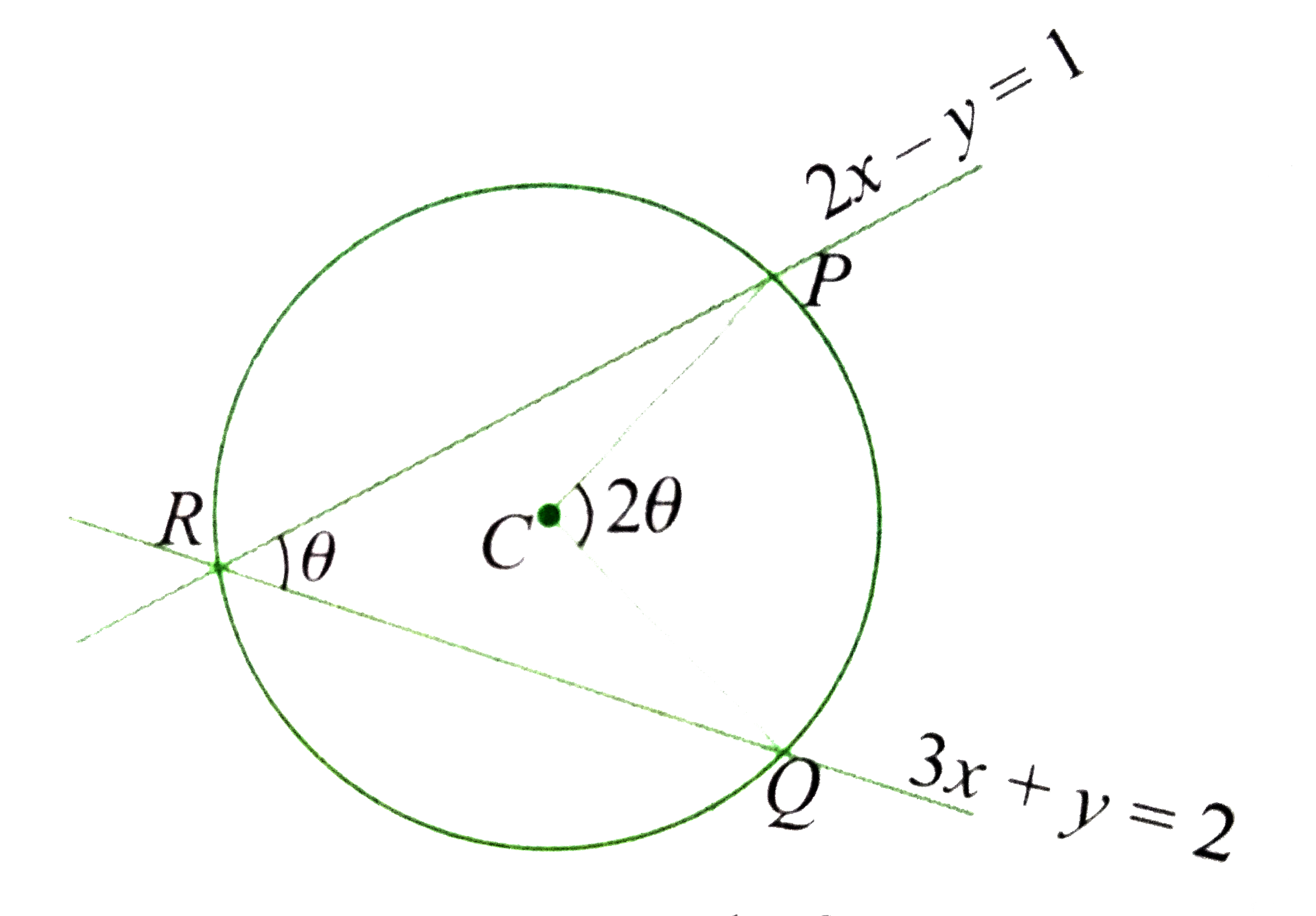
Slopes of gives lines are 2 and $- 3$ .
If angle between lines is $θ$ , then
$tan θ = ∣ ∣ ∣ \frac{2 - (- 3)}{1 + (2) \times (- 3)} ∣ ∣ ∣ = 1$
$∴ θ = ∠ P R Q = 45^{\circ}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
What is the point of intersection of the lines $x - 3 = 0$ and y- 5 = 0?
A(-3,5)
B(-3,-5)
C(3,5)
D(3,-5)
Question 2 - Select One
What is the point of intersection of the lines x-3 = 0 and y- 5 = 0?
A(-3,5)
B(-3,5)
C(3,5)
D(3,-5)
Question 3 - Select One
Point of intersection of two lines 3x+2y-7=0 and 5x+3y-11=0 is
A(1,2)
B(2,1)
C(-1,-2)
D(-2,-1)

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile