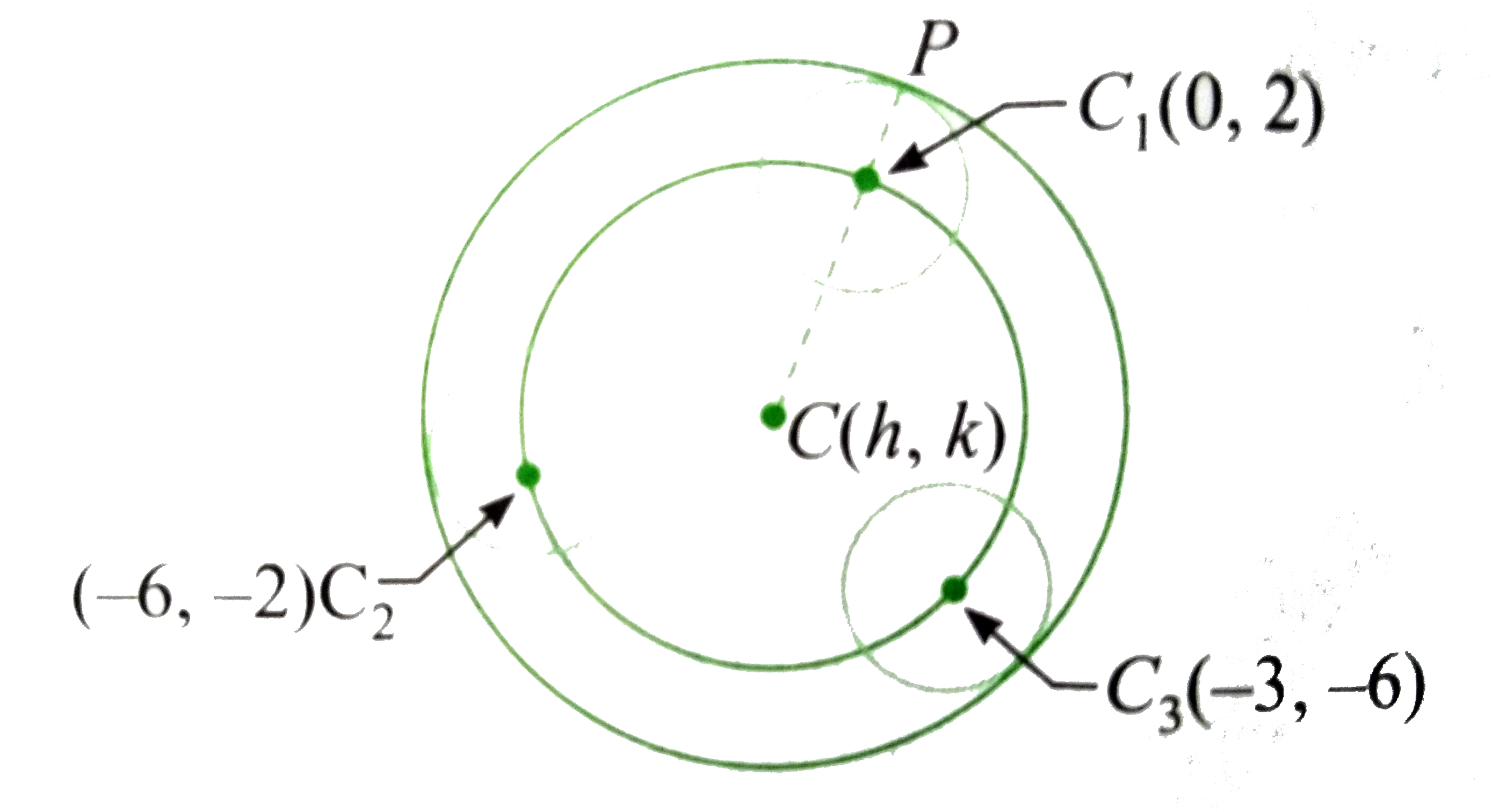
The minimum radius of the circle which contains the three circles, $x^{2} + y^{2} - 4 y - 5 = 0, x^{2} + y^{2} + 12 x + 4 y + 31 = 0$ and $x^{2} + y^{2} + 6 x + 12 y + 36 = 0$ is

A

$\frac{7}{18} \sqrt{900} + 3$

B

$\frac{\sqrt{845}}{9} + 4$

C

$\frac{5}{36} \sqrt{949} + 3$

D

none of these

Text Solution

Verified by Experts

The correct Answer is:3

$S_{1} \equiv x^{2} + y^{2} - 4 y - 5 = 0$
$S_{2} \equiv x^{2} + y^{2} + 12 x + 4 y + 31 = 0$
and $S_{3} \equiv x^{2} + y^{2} + 6 x + 12 y + 36 = 0$
$C_{1} \equiv (0, 2), r_{1} = 3$
$C_{2} \equiv (- 6, - 2), r_{2} = 3$
$C_{3} \equiv (- 3, - 6), r_{3} = 3$

All circles have the same radius,
The radius of the circle touching all the circles is
$C P = C C_{1} = C_{1} P + 3$
Let $C (h, k)$ be the center of the required circle. Then,
$C C_{1} = C C_{2} = C C_{3}$ or $C C_{1}^{2} = C C_{2}^{2} = C C_{3}^{2}$
or ${(h - 0)}^{2} + {(k - 2)}^{2} = {(h + 6)}^{2} + {(k + 2)}^{2}$
$= {(h + 3)}^{2} + {(k + 6)}^{2}$
or $- 4 k + 4 = 12 h + 4 k + 40 = 6 h + 12 k + 45$
or $3 h + 2 k + 9 = 0$ and $6 h - 8 k - 5 = 0$
Solving, we get
$h = \frac{- 31}{18}, k = \frac{- 23}{12}$
$∴ C C_{1} = \sqrt{{(0 + \frac{31}{18})}^{2} + {(2 + \frac{23}{12})}^{2}} = \frac{5}{36} \sqrt{949}$
Now, $C P = C C_{1} + 3 = \frac{5}{36} \sqrt{949} + 3$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of a circle which cuts the three circles $x^{2} + y^{2} + 2 x + 4 y + 1 = 0, x^{2} + y^{2} - x - 4 y + 8 = 0$ and $x^{2} + y^{2} + 2 x - 6 y + 9 = 0$ orthogonlly is
A $x^{2} + y^{2} - 2 x - 4 y + 1 = 0$
B $x^{2} + y^{2} + 2 x + 4 y + 1 = 0$
C $x^{2} + y^{2} - 2 x + 4 y + 1 = 0$
D $x^{2} + y^{2} - 2 x - 4 y - 1 = 0$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile