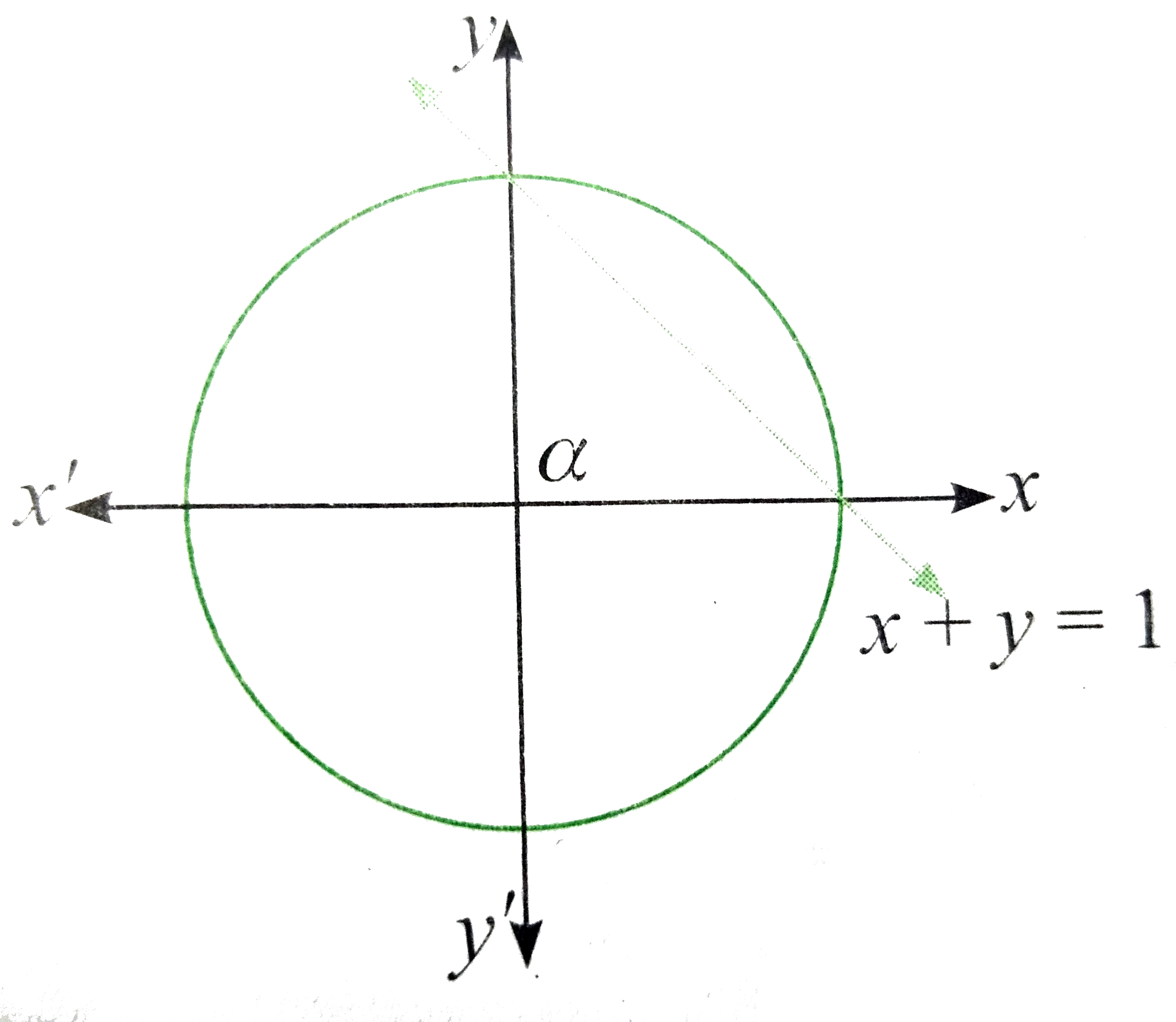
Let $α$ chord of a circle be that chord of the circle which subtends an angle $α$ at the center.
If $x + y = 1$ is a chord of $x^{2} + y^{2} = 1$ , then $α$ is equal to

A

$π / 4$

B

$π / 2$

C

$π / 6$

D

$x + y = 1$ is not a chord

Text Solution

Verified by Experts

The correct Answer is:2

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Let $α$ chord of a circle be that chord of the circle which subtends an angle $α$ at the center.
If the slope of a $π / 3$ chord of $x^{2} + y^{2} = 4$ is 1, then its equation is
View Solution
Let $α$ chord of a circle be that chord of the circle which subtends an angle $α$ at the center.
The distance of $2 π / 3$ chord of $x^{2} + y^{2} + 2 x + 4 y + 1 = 0$ from the center is
View Solution

Knowledge Check

If $α -$ chord of a circle be that chord which subtends an angle $α$ at the centre of the circle.
If x+y=1 is $α$ -chord of $x^{2} + y^{2} = 1$ , then $α$ is equal to
A $\frac{π}{6}$
B $\frac{π}{4}$
C $\frac{π}{2}$
D $\frac{3 π}{4}$
Let $α$ chord of a circle be that chord of the circle which subtends an angle $α$ at the center.
If the slope of a $π / 3$ chord of $x^{2} + y^{2} = 4$ is 1, then its equation is
A $x - y + \sqrt{6} = 0$
B $x - y = 2 \sqrt{3}$
C $x - y = \sqrt{3}$
D $x - y + \sqrt{3} = 0$
Let $α$ chord of a circle be that chord of the circle which subtends an angle $α$ at the center.
The distance of $2 π / 3$ chord of $x^{2} + y^{2} + 2 x + 4 y + 1 = 0$ from the center is
A1
B2
C $\sqrt{2}$
D $1 / \sqrt{2}$

CENGAGE-CIRCLE -Exercise (Comprehension)

Home
Ask Doubt
Profile