Let A(−4,0),B(4,0) Number of points c=(x,y) on circle x2+y2=16 such that area of triangle whose verties are A,B,C is positive integer is:
The correct Answer is:62
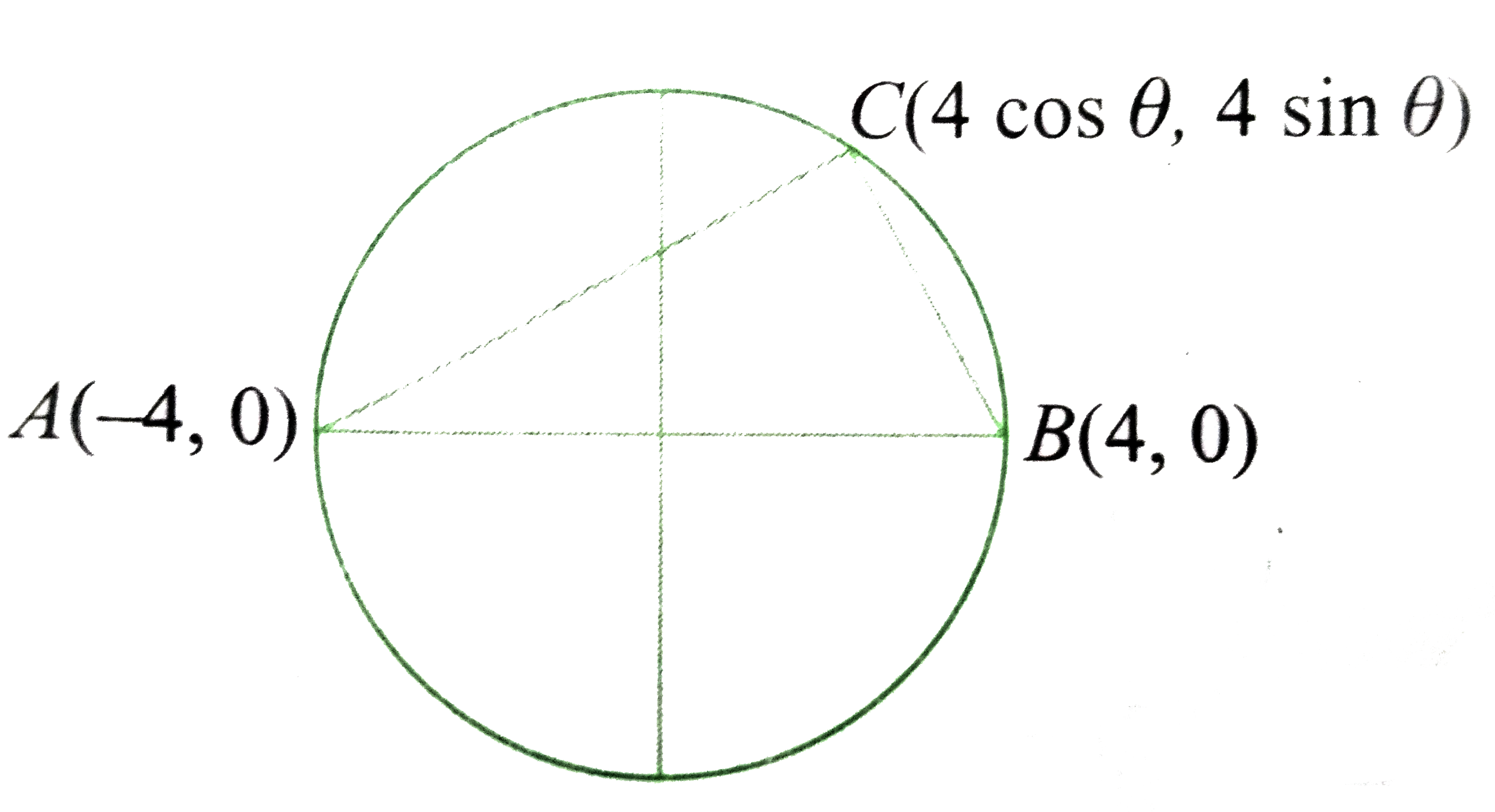
Required area
A=12×8×|4sinθ|=|16sinθ|
Now, the area is an integer. Then the possible values of sinθ are
116,216,.....,1516
i.e., 15 points in each quadrant or 60+2 more with sinθ=1.
Therefore,N=62 lt
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Main Previous Year10videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)14videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)1videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank32videos
CIRCLES
Similar Questions
let A(−4,0),B(4,0) number of points c=(x,y) on circle x2+y2=16 such that area of triangle whose vertais one A,B,C is positive integer :
View SolutionLetA (-4.0) and B (4.0). Number of points C (x.y) on the circle x +y -16 such that the areaof the triangle whose vertices are A.Band Cisapositive integer, is
View Solution
Knowledge Check
- Question 1 - Select One
Let A (2,3),B(4,5) be two points and let C=(x,y) be a point such that (x−2)(x−4)+(y−3)(y−5)=0 If area of ΔABC=√2aq. Units, then find the maximum number of positions of C in the xy plane.
A1B2C3D4 - Question 2 - Select One
Let B and C are points of interection of the parabola y=x2 and the circle x2+(y−2)2=8. The area of the triangle OBC, where O is the origin, is
A2B4C6D8
Let A=(1,2),B=(3,4)andC=(x,y) lie on the circumcircle of triangle ABC having AB as a diameter such that area of triangle ABC=1 the maximum number of position of C in the x-y plane is:
View SolutionLet A(1, 2), B(3, 4) be two points and C(x, y) be a point such that area of ΔABC is 3 sq. units and (x−1)(x−3)+(y−2)(y−4)=0. Then number of positions of C, in the xy plane is
View SolutionA tangent to the elise x24+y21=1 cuts the circle x2+y2=4 at points A and B, C any point on the circle x2+y2=4 such that A, B and C are to the same side of x-axis. Find the maximum area of the triangle ABC.
View SolutionLet (a, b) is the midpoint of the chord AB of the circle x2+y2=r2. The tangents at A and B meet at C, then the area of triangle ABC
View SolutionLet A(2,3),B(4,5) and let C=(x,y). be a point such that (x−2)(x−4)+(y−3)=0. If area of △ABC=√2 sq. unit, then maximum nunber of positions of C in the xy plane is
View SolutionGiven 2 fixed points A(2,4) and B(5,1). A variable point P is taken on the circle x2+y2=1, then number of integer(s) in the range of area of ΔAPB are
View Solution

