Find the area between the ellpise x2a2+y2b2=1 and lines |x|a+|y|b=1
Video Solution
Text Solution
Given ellips is Find the area between the ellpise x2a2+y2b2=1
Given lines |x|a+|y|b=1 formed a parallelogram whose diagonals are major axes of the given ellips.
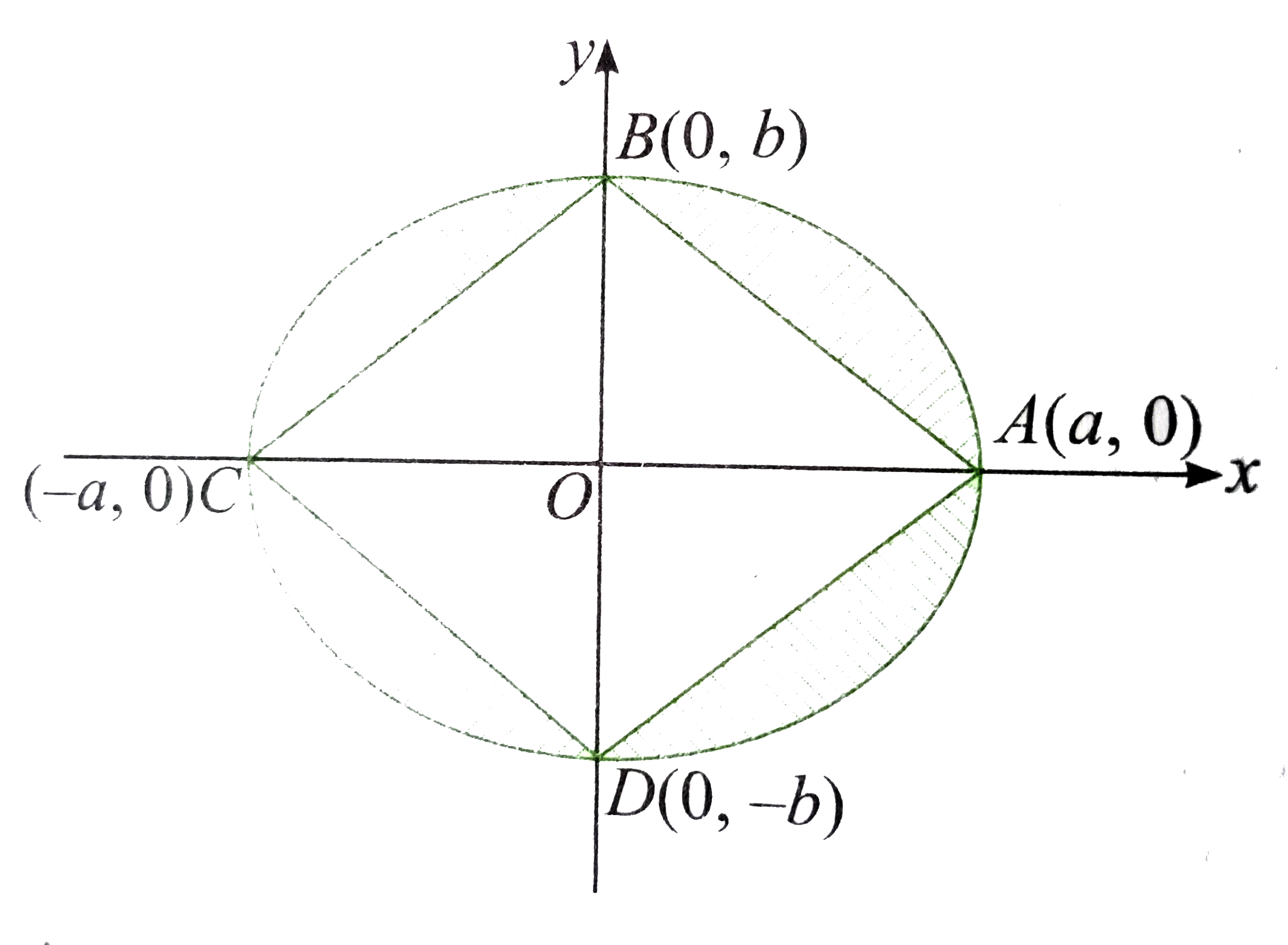
Required region shaded region in the figure.
∴ Required area= Area of ellipse-Area of paralllogram
=πab−4×12ab=(π−2)ab
|
Similar Questions
Knowledge Check
The area of the ellipse x2a2+y2b2=1 is
AπabBπ4(a2+b2)Cπ(a+b)Dπa2b2The area of the ellipse x2a2+y2b2=1 is
AπabBπ(a2+b2)/4Cπ(a+b)DNoneArea of the region bounded by the curve {(x,y):x2a2+y2b2≤1≤xa+yb} is
A(π4−12)abB(π4+12)abC(π4−13)abDπ4ab
Find the area between the curve x2a2+y2b2=1and the x-axis between x=0andx=a. Draw rough sketch of the curve also.
View SolutionFind the area between the curves y=x2 and x=y2.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionFind the maximum area of the ellipse x2a2+y2b2=1 which touches the line y=3x+2.
View Solution
