An ellipse is inscribed in a reactangle and the angle between the diagonals of the reactangle is ${tan}^{- 1} (2 \sqrt{2})$ , then find the ecentricity of the ellipse

Text Solution

Verified by Experts

The correct Answer is: $\frac{1}{\sqrt{2}}$

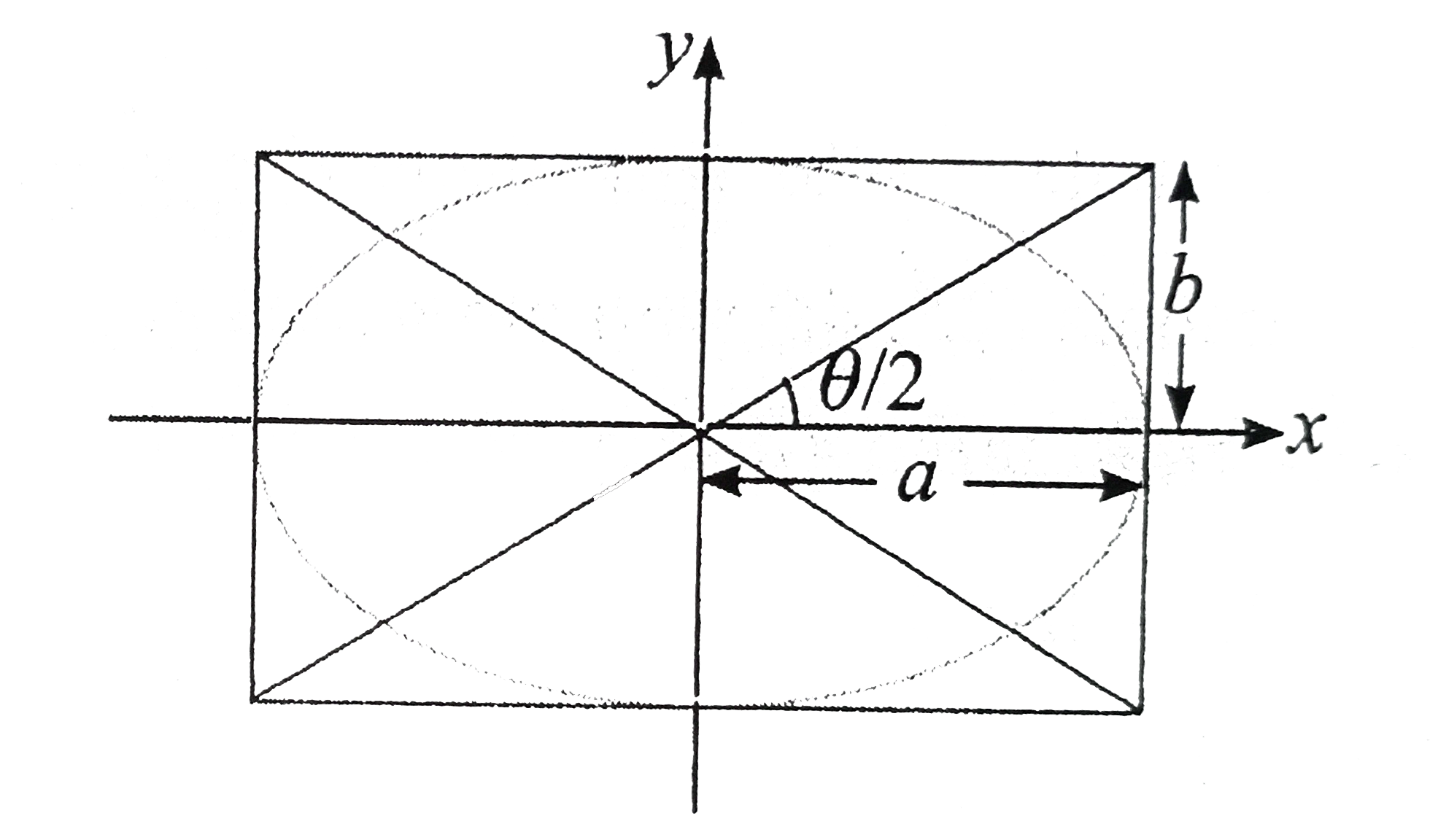
From the figure, we have
$tan . \frac{θ}{2} = \frac{b}{a} \Rightarrow {tan}^{2} . \frac{θ}{2} = \frac{b^{2}}{a^{2}}$
$\Rightarrow \frac{1 - cos θ}{1 + cos θ} = \frac{b^{2}}{a^{2}}$
$\Rightarrow \frac{1 - \frac{1}{3}}{1 + \frac{1}{3}} = \frac{b^{2}}{a^{2}} \Rightarrow \frac{b^{2}}{a^{2}} = \frac{1}{2}$
$∴ e = \sqrt{1 - \frac{b^{2}}{a^{2}}} = \frac{1}{\sqrt{2}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
Ellipse $x^{2} + 4 y^{2} = 4$ is inscribed in a rectangle aligned with co-ordinate axes . This rectangle itself is inscribed in another ellipse the passes ellipse that through (-4,0) . Then the equation of the ellipse is
A $x^{2} + 16 y^{2} = 16$
B $x^{2} + 12 y^{2} = 16$
C $4 x^{2} + 48 y^{2} = 48$
D $4 x^{2} + 64 y^{2} = 48$

Recommended Questions

Home
Ask Doubt
Profile