Let P be a pooint on the ellipse x2a2+y2b2=1(a>b) in the first or second quadrants whowse foci are S1andS2. Then the least possible value of circumradius of ΔPS1S2 will be
A
ae
B
be
C
aeb
D
ae2b
Text Solution
We known that circumradius of triangle
R=Product of all sides4×Area of triangle ltbr Consider point P(acosθ,bsinthea) on the ellipse.
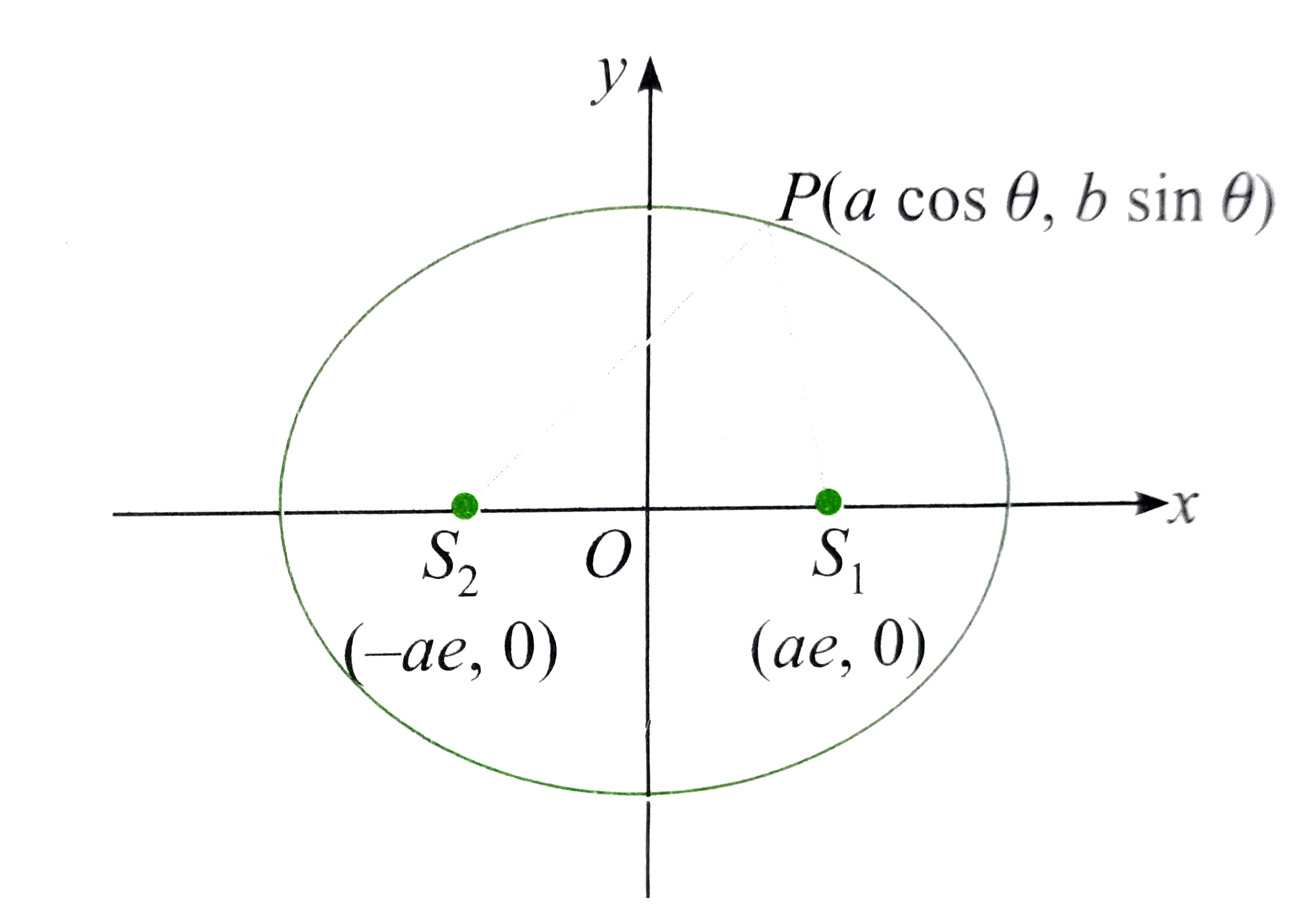
∴ Circumrdius , R=a(1−ecosθ)×a(1+ecosθ)×2ae4×12bsinθ×2ae
=a2(1−e2cos2θ)2bsinθ
=a2(1−e2(1−sin2θ))2bsinθ
=a22(e2sinθ+b2a2cosecθ)
≥a22b×2beaae
∴Rmin=a22b×2bea=ae
|
Similar Questions
Knowledge Check
P is any point on the ellipise x2a2+y2b2=1 and S and S are its foci, then maximum value of the angle SPS is
Aπ4Bπ2Ctan−1aebDnone of theseIf P(θ) is a point on the hyperbola x2a2−y2b2=1, whose foci are S and S', then SP.S'P=
Aa2sec2θ+b2tan2θBa2sec2θ−b2tan2θCa2tan2θ−b2sec2θDa2tan2θ+b2sec2θLet P be a variable point on the elipse x2a2+y2b2=1 with foci F1andF2. If A is the area of the triangle PF1F2, then maximum value of A is
AabeBabe(c)C2abeDnone
If P is a point on the ellipse x236+y29=1, S and S ’ are the foci of the ellipse then find SP+S1P
View SolutionLet P be a variable point on the ellipse x225+y216=1 with foci at S and S'. Then find the maximum area of the triangle SPS'
View SolutionP is any point lying on the ellipse x2a2+y2b2=1(a>b) whose foci are S and S'. If ∠PSS'=aand∠PS'S=β, then the value of tan.α2tan.β2 is
View SolutionConsider any point P on the ellipse x225+y29=1 in the first quadrant. Let r and s represent its distances from (4, 0) and (-4, 0) respectively, then (r + s) is equal to:
View SolutionIf P is a point on the ellipse X29+y24=1
whose foci are S and S' then the value of PS + PS' is
View Solution
