An ellipse $E, \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , centred at point O has AB and CD as its major and minor axes, respectively. Let $S_{1}$ be one of the foci of the ellipse, the radius of the incircle of traingle $O C S_{1}$ be 1 unit, adn $O S_{1} = 6$ units
The equation of the director circle of E is

$x^{2} + y^{2} = 48.5$

$x^{2} + y^{2} = \sqrt{97}$

$x^{2} + y^{2} = 97$

$x^{2} + y^{2} = \sqrt{48.5}$

Text Solution

Verified by Experts

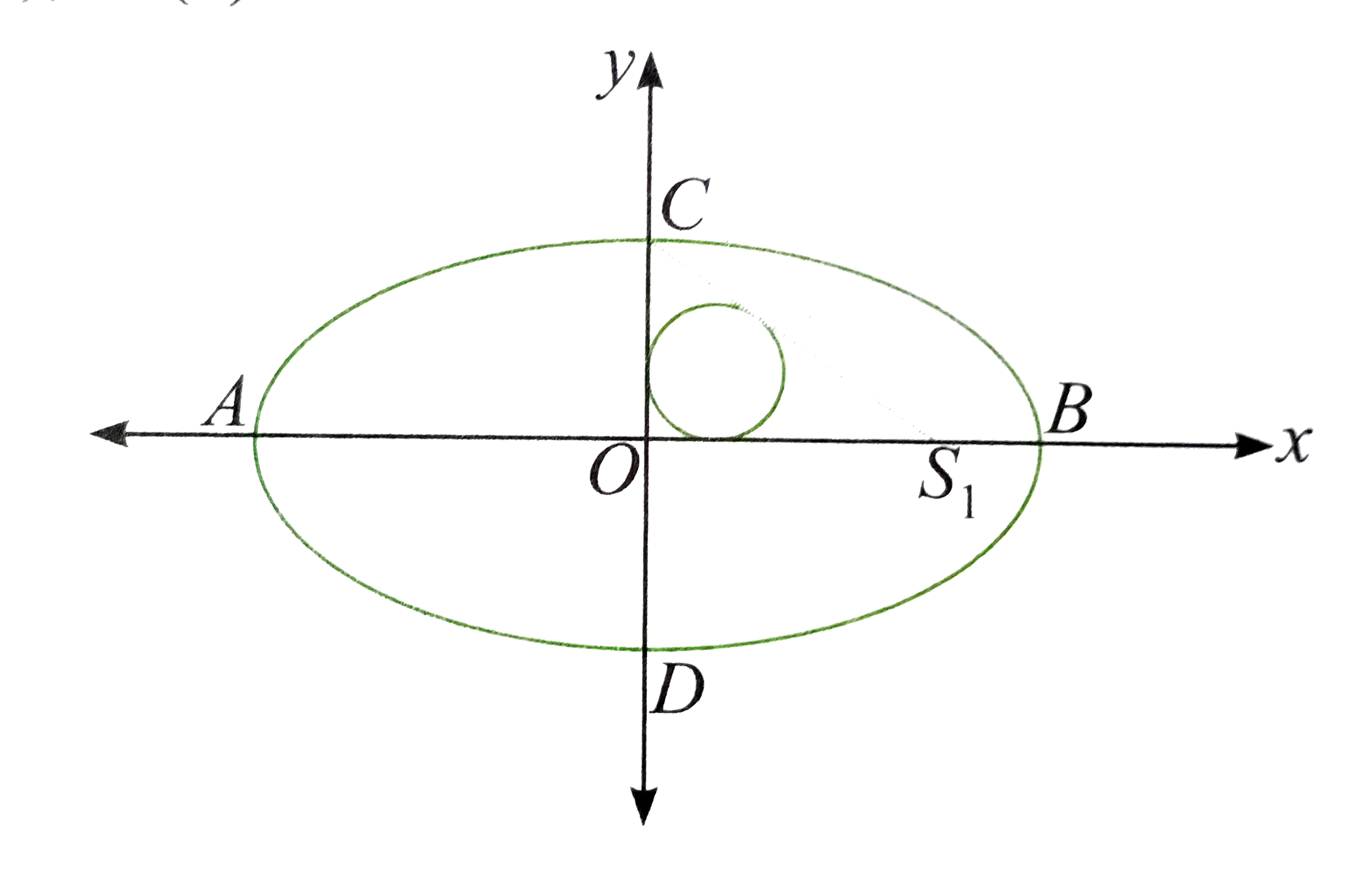
$∴ O S_{1} = a e = 6, O C = b$
Also, $C S_{1} = a$
$∴ Area of Δ O C S_{1} = \frac{1}{2} = (O S_{1}) \times (O C) = 3 b$
$∴$ Semi-perimeter of $Δ O C S_{1} = \frac{1}{2} = (O S_{1} + O C + C S_{1})$
$= \frac{1}{2} (6 + a + b) (1)$
$∴$ In radius of $Δ O C S_{1}, (Using r = \frac{Δ}{S})$
= $\frac{3 b}{\frac{1}{2} (6 + a + b)} = 1 (Using r = \frac{Δ}{S})$
$or 5 b = 6 + a (2)$
Also, $b^{2} = a^{2} - a^{2} e^{2} = a^{2} - 36 (3)$
From (2), we get
$25 (a^{2} - 36) = 36 + a^{2} + 12 a$
$or 2 a^{2} - a - 78 = 0$
$a = \frac{13}{2}, - 6$
$∴ a = \frac{13}{2} and b = \frac{5}{2}$
Area or ellipse $= π a b = \frac{65 π}{4}$ sq. unit
Perimeter of $Δ O C S_{1} = 6 + a + b = 6 + \frac{13}{2} + \frac{5}{2} = 15$ units
The equation of director circle is
$x^{2} + y^{2} = a^{2} + b^{2}$
or $x^{2} + y^{2} = \frac{97}{2}$

An ellipse $E, \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , centred at point O has AB and CD as its major and minor axes, respectively. Let $S_{1}$ be one of the foci of the ellipse, the radius of the incircle of traingle $O C S_{1}$ be 1 unit, adn $O S_{1} = 6$ units
The area of ellipe (E) is
A $65 π / 4$
B $64 π / 5$
C $64 π$
D $65 π$
An ellipse $E, \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , centred at point O has AB and CD as its major and minor axes, respectively. Let $S_{1}$ be one of the foci of the ellipse, the radius of the incircle of triangle $O C S_{1}$ be 1 unit, and $O S_{1} = 6$ units The perimeter of $Δ O C S_{1}$ is
A20 units
B10 units
C15 units
D25 units
Consider an ellipse E: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , centered at point 'O' and having AB and CD as its major and minor axes respectively if $S_{1}$ be one of the focus of the ellipse, radius of the incircle of $Δ O C S_{1}$ be 1 unit and $O S_{1} = 6$ units.
Q. if the ellipse (E) is ∆sq unit, then the value of 4 $Δ$ is
A $63 π$
B $64 π$
C $65 π$
D $66 π$