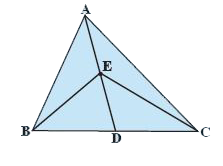
In a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
 Solution in Tamil
Solution in Tamil
Step by step video & image solution for In a triangle ABC (see figure), E is the midpoint of median AD, show that (i) ar DeltaABE = ar DeltaACE (ii) ar DeltaABE=1/4ar(DeltaABC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The area of parallelogram ABCD is 36cm2 . Calculate the height of parallelogram ABEF if AB = 4.2 cm

View SolutionIf x3+6x2+kx+6 is exactly divisible by (x+2), then k=?
View SolutionFind the values of x and y in the figures given below

View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionΔABC में, E मध्यिका AD का मध्य - बिंदु है । दर्शाइए कि ar(BED)=14ar(ABC) है।
View SolutionΔABC में, E माध्यिका AD का मध्य-बिन्दु है। दर्शाइए कि ar(BED)=14ar(ABC) है।
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View SolutionMatch column I with column II:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C18_E01_003_Q01.png" width="80%"gt
View Solution△ABC में, E माध्यिका AD का मध्य -बिन्दु है । दर्शाइए कि -
ar(BED)=14ar(ABC)
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
View Solution
