A hemisphere is cut from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the side of the cube. Determine the total surface area of the remaining solid.Solution in Tamil
The correct Answer is:x2(π+244) sq. units
Step by step video, text & image solution for A hemisphere is cut from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the side of the cube. Determine the total surface area of the remaining solid. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NCERT TAMILCHAPTER - MENSURATIONEXERCISE - Exercise 10.37videos
MENSURATION
- BOOK - NCERT TAMILCHAPTER - MENSURATIONEXERCISE - Exercise 10.48videos
MENSURATION
- BOOK - NCERT TAMILCHAPTER - MENSURATIONEXERCISE - Unit Exercise - 710videos
MENSURATION
- BOOK - NCERT TAMILCHAPTER - GEOMETRYEXERCISE - UNIT EXERCISE - 45videos
GEOMETRY
- BOOK - NCERT TAMILCHAPTER - NUMBERS AND SEQUENCES EXERCISE - Unit Exercise - 210videos
NUMBERS AND SEQUENCES
Similar Questions
A iron pillar consists of a cylindrical portion of 2.8 m height and 20 cm in diameter and a cone of 42 cm height sumounting it. Find the weight of the pillar if 1 cm3 of iron weights 7.5 g.
02:53View SolutionA metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6cm. Find the height of the cylinder.
06:32View SolutionThe barrel of a fountain-pen cylindrical in shape, is 7 cm long and 5 cm in diameter. A full barrel of ink in the pen will be used for writing 330 words on an average. How many words can be written using a bottle of ink containing one fifth of a litre ?
03:56View SolutionIn the given figure AB||CD||EF.
If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
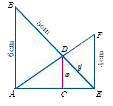 04:06View Solution
04:06View SolutionProve that n2−n divisible by 2 for every positive integer n.
05:26View SolutionA hemispherical depression is cut out from one face of a cubical wooden block such that the diameter lof the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
06:13View SolutionA hemispherical depression is cut out from one face of a cubical wooden plank such that the diameter 4 of the hemisphere is equal to the edge of the cube.Determine the surface area of remaining solid.
03:42View SolutionA hemispherical depression is cut out from one face of a cubical wooden block such that the diameter ‘l’ of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
06:32View SolutionA hemispherical depression is cut out from one face of a cubical block of side 7cm, such that the diameter of the hemisphere is equal to the edge of the cube.Find the surface area of the remaining solid.
06:41View SolutionA hemispherical depression is cut-out from one face of the cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
View SolutionA hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
04:19View SolutionA hemisphere is cut out from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
04:22View SolutionA hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
02:36View SolutionA hemisphere is cut from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the side of the cube. Determine the total surface area of the remaining solid.
06:51View SolutionA hemisphere is cut from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the side of the cube. Determine the total surface area of the remaining solid.
03:58View Solution

