In a human pyramid in a circus, the entire weight of the balanced group is supported by the legs of a performer who is lying on his back (as shown in Fig. 9.5). The combined mass of all the persons performing the act, and the table, plaques etc. involved is 280 kg. The mass of the performer lying on his back at the bottom of the pyramid is 60 kg. Each thighbone (femur) of this performer has a length of 50 cm and an effective radius of 2.0 cm. Determine the amount by ehich each thighbone gets compressed under the extra load.

Total mass of all performers, tables plaques etc. = 280 kg
Mass of the performer = 60 kg
Mass supported by the legs of the performer at the bottom of the pyramid
=280−60=220 kg
Weight of this supported mass
=220 kg wt.=220×9.8 N = 2156 N.
Weight supported by each thighbone of th performer =1/2(2156)N=1078N.
From Table 9.1, the Young.s modulus for bone is given by
Y =9.4×109N m−2.
Length of each thighbone L=0.5 m
the radius of thighbone =2.0cm
Thus the cross - sectional area of the thighbone
A=π×(2×10−2)2m2=1.26×10−3m2.
Using Eq. (9.8), the compression in each thighbone (ΔL) can be computed as
ΔL=[(F×L)/(Y×A)]
=[(1078×0.5)/(9.4×109×1.26×10−3)]
=4.55×105 m or 4.55×10−3 cm.
This is very small change! The fractional decrease in the thighbone is ΔL/L=0.000091 or 0.0091%
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDS Book:NCERT TAMILChapter:MECHANICAL PROPERTIES OF SOLIDS Exercise:Exercises
Explore 21 Videos
- MECHANICAL PROPERTIES OF FLUIDS Book:NCERT TAMILChapter:MECHANICAL PROPERTIES OF FLUIDS Exercise:EXERCISE
Explore 45 Videos
- MOTION IN A PLANEBook:NCERT TAMILChapter:MOTION IN A PLANEExercise:EXCERCISES
Explore 32 Videos
Similar Questions
In a human pyramid in a circus, the entire weight of the balanced group is supported by the legs of a performer who is lying on his back (as shown in Fig. 9.5). The combined mass of all the persons performing the act, and the tables, plaques etc. involved is 280 kg and of each person is 60 kg. Each thighbone (femur) of this performer has a length of 50 cm and an effective radius of 2.0 cm. Determine the amount by which each thighbone gets compressed under the extra load.
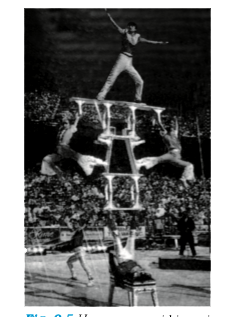
View SolutionIn a human pyramid in a circus, the entire weight of the balanced group is supported by the legs of a performero who is lying on his back (as shown in Fig. 9.5). The combined mass of all the persons performing the act, and the tables, plaques etc. involved is 60 kg. Each thighbone (femur) of this performer has a length of 50 cm and an effective radius of 2.0 cm. Determine the amount by which each thighbone gets compressed under the extra load.
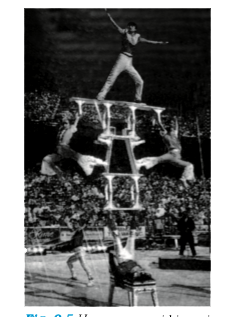
View Solution
Knowledge Check
A man has mass 70 kg and the mass of his wife is 50 kg. The ratio of the inertia of the man to the inertia of his wife is
A5:7B1:2C7:5D1:3
A father has mass 60 kg and the mass of his on is 30 kg . What is the ratio of inertia of the father to the inertia of his son ?
View SolutionHis performance is fairly unsatisfactory.
View SolutionHis performance is rather satisfactory.
View Solution(a) a person weighs 60 kg on earth. Will his weight increase as he moves to the top of a hill ?
(b) will the weight of person increase at the bottom of a mine ?
View Solution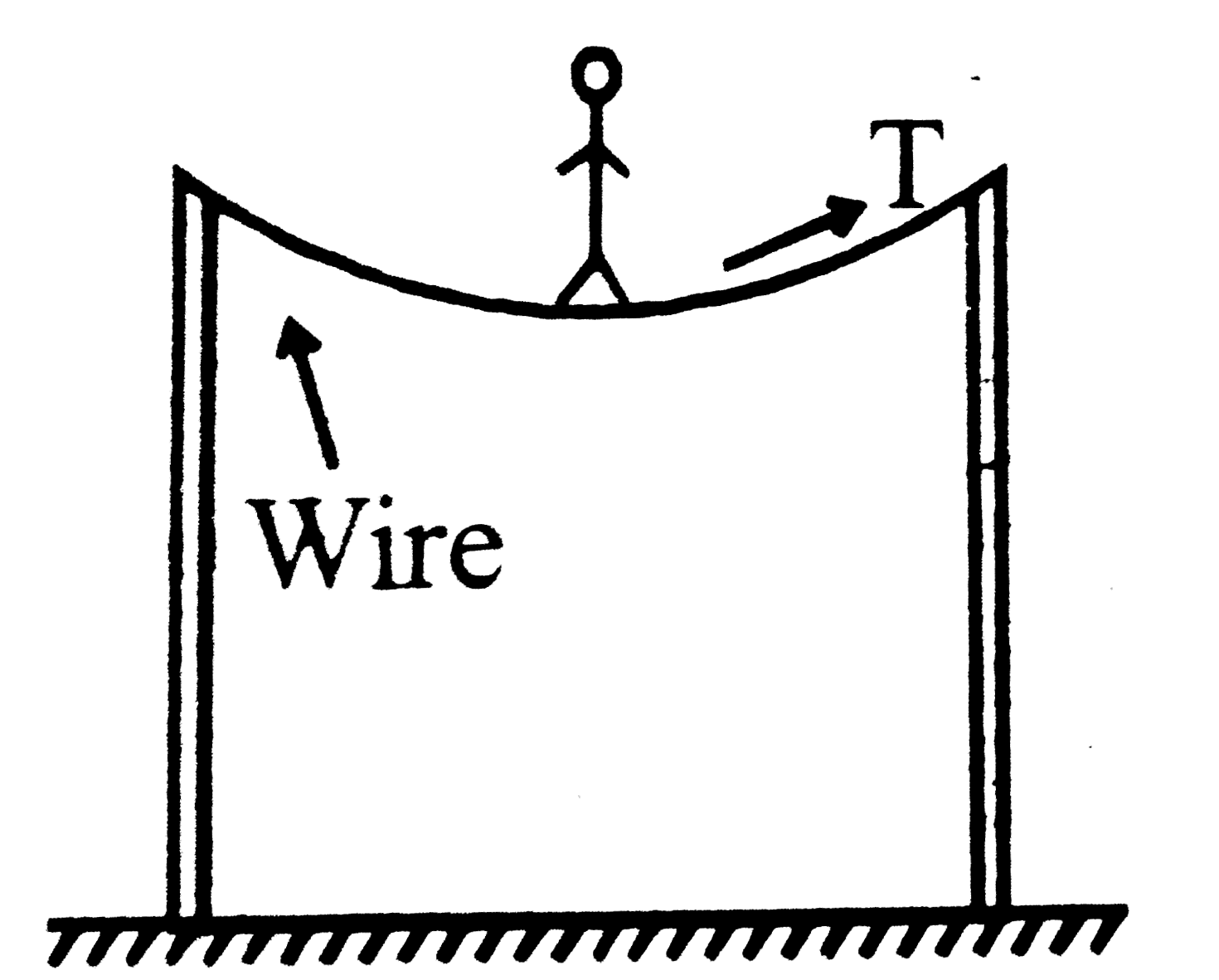
A circus performer of mass M is walking along a wire as shown in the figure given above. The tension T in the wire is (g = acceleration due to gravity)
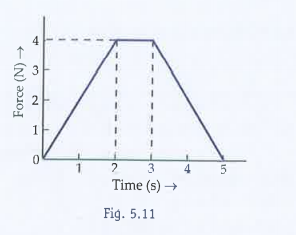
View SolutionA force acting on a body of mass 2 kg varies with time as shown in fig.5.11. Find impulse of the force.
View SolutionWrite the truth table for the circuit shown in Fig. Name the gate of which this circuit is performing.
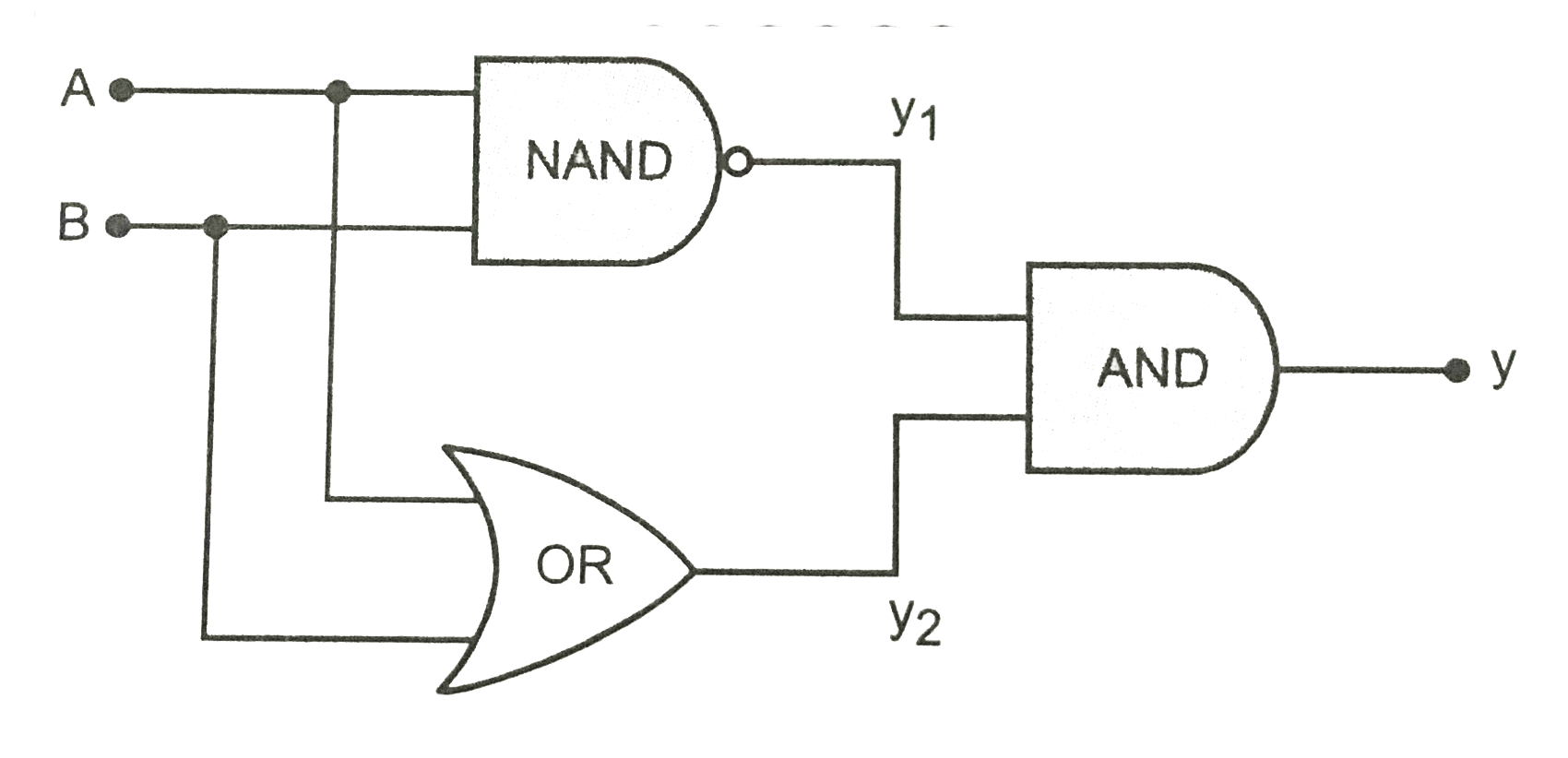
View Solution
