A line charge lambda per unit length is lodged uniformly onto the rim

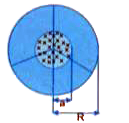
A line charge $λ$ per unit length is pasted uniformly on to the wire of a wheel of mass $m$ and radius $R$ . The wheel has light non-conducting spokes and is free to rotate about a vertical axis as shown in $F i g . 3.166$ . A uniform magnetic field extends over a radial rigion of radius $r$ given by $B = - B_{0} ˆ k (r \leq a, a < R) = 0$ (otherwise). What is the angular velocity of the wheel this field is suddenly switched off?

A(a) $\frac{- 2 B_{0} π a^{2} r}{m R} ˆ k$
B(b) $\frac{- 2 B_{0} π a^{2} r}{3 m R} ˆ k$
C( c) $\frac{B_{0} π a^{2} λ}{m R} ˆ k$
D( d) $\frac{- B_{0} π a^{2} λ}{m R} ˆ k$
A non-conducting ring of radius r has charge per unit length $λ$ . A magnetic field perpendicular to plane of the ring changes at rate Db/dt. Torque experienced by the ring is

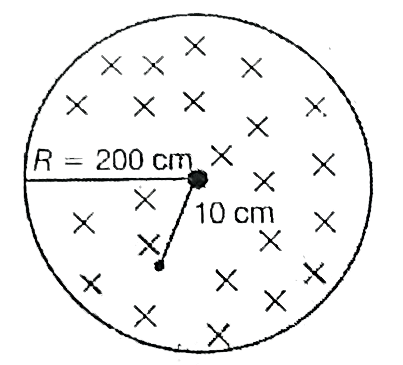A $λ π r^{3} \frac{d B}{d t}$
B $λ 2 π r^{3} \frac{d B}{d t}$
C $λ^{2} {(2 π r)}^{2} \frac{d B}{d t}$
Dzero
A conducting solid sphere having uniform charge Q on it has radius R. It is rotating with anangular velocity ω. If a uniform magnetic field B is present perpendicular to axis of rotation then the torque on sphere will be
A $\frac{q ω R^{2}}{5} B$
B $\frac{q ω R^{2}}{3} R$
C $\frac{q ω R^{2}}{4} B$
D $\frac{q ω R^{2}}{2} R$

$- \frac{B π a^{2} λ}{M R} ˆ k$